Dans la maîtrise statistique des procédés de technologie de montage en surface, le Cpk est le roi.

Allons revoir Patty et l'équipe......

Il y a plusieurs semaines...

C'était juste avant Noël et Patty se dirigeait vers l'Ivy League depuis sa maison à Woodstock dans le Vermont. Alors qu'elle passait devant la bibliothèque, elle vit le groupe HS de Woodstock jouer des chants de Noël. Heureusement, il y avait une place de stationnement à proximité. Ainsi, elle arrêta sa voiture et sortit pour prendre une vidéo avec son iPhone 6S

pour la montrer ensuite à Rob et les garçons. Après quelques minutes d'enregistrement, elle s'apprêta à ranger son téléphone portable, mais ses doigts étaient froids et elle le laissa tomber sur le ciment gelé. Le téléphone a été baptisé avec sa première bosselure. Patty gémit. Dans leur quête pour fabriquer le téléphone le plus mince, Apple l'a rendu pratiquement impossible à tenir sans une couverture tactile.

Aujourd’hui...

Patty se précipitait à son bureau comme elle avait une réunion avec Pete. Son dernier texte avait l'air urgent.

Comme elle était presque arrivée, elle vérifia sa charge Fitbit® et sa montre Apple. Elle comparait leurs applications de conditionnement physique à une conférence qu'elle donnait à ENGS 1 « technolie pour tous les jours » à l'Ivy League. Il se trouvait que le Fitbit donnait un nombre de pas plus précis ; la montre Apple manquait les foulées moins vigoureuses et elle ne comptait pas les volées d'escaliers. Cependant, une égratignure sur le cristal du Fitbit est apparue récemment (le cristal n'était-il pas du saphir ?). Elle se demandait si le prix de 150 $ US était raisonnable pour un dispositif qui n'avait pas beaucoup de fonctions. Certes, la montre Apple coûtait environ 350 $, mais elle pouvait faire beaucoup de choses.

Comme Patty approchait de son bureau, Pete était assis dehors et semblait stressé.

« Quoi de neuf ? » demanda Patty.
« Je viens de recevoir un courriel de Mike Madigan posant de nouvelles questions sur les Cp et Cpk », répondit Pete.
« Ça ne devrait pas être un problème. » répondit Patty.
« Non. Mais moi, donner une conférence sur les Cp et Cpk ! » Dit Pete avec un regard inquiet.
« Tu as tellement parlé de mon travail sur ces sujets et de ma feuille de calcul Excel que le professeur Walters m'a demandé de discuter de tout cela dans sa classe de statistiques. » Continua Pete.
« Et le problème est ? » demanda Patty.
« J'ai peur de parler devant un groupe de personnes », avoua Pete.

Patty fit une pause. Autant qu'ils avaient travaillé ensemble, elle ne l'avait jamais vu parler devant un groupe. Ils ont passé les 10 minutes suivantes à élaborer un plan pour aider Pete à surmonter cet obstacle.

« Arrives-tu à parler à Mike seul ? » Patty changea de sujet.
« Certainement ! Ça je peux le faire », rétorqua Pete.
Pete alla à son bureau et relut le courriel de Mike.

   Pete, merci pour votre feuille de calcul Excel au sujet de Cp et Cpk. Une chose que nous ne comprenons pas, c'est la différence entre les défaillances unilatérales et bilatérales. Peux-tu m'appeler pour qu'on en parle ? Pourquoi pas aujourd'hui à 16h ? Cordialement, Mike.
Pete avait utilisé Minitab^®

pour mettre au point des graphiques qui expliquent la différence entre les défauts unilatéraux et bilatéraux. À midi, il était prêt pour sa téléconférence avec Mike. Le reste de la journée passa vite car il avait plusieurs réunions avec des étudiants jusqu'à son appel de 16 heures.

A 15h59, Pete composa le numéro de Mike.

« Salut Pete ! Merci de m'appeler. Notre équipe est impressionnée par votre Cp et Cpk feuille de calcul, mais nous ne comprenons pas la différence entre les défauts unilatéraux et bilatéraux. Pouvez-vous éclaircir ça pour moi ? » Commença Mike.

« Bien-sûr. Jetez un œil au PowerPoint que je vous ai envoyé. Il montre des distributions pour deux échantillons d'alésages. La recommandation est 1,00 mm +/- 0,06 mm. En règle générale, nous nous attendons à ce que la recommandation soit à une limite de 3 sigmas, donc le sigma devrait être 0,02 mm. Notez qu’une des distributions a une moyenne au centre (1,00 mm), mais le sigma est de 0,03, supérieur à celui souhaité. L'autre distribution a le sigma souhaité de 0,02 mm, mais la moyenne est décalée vers 0,974 mm », commença Pete.

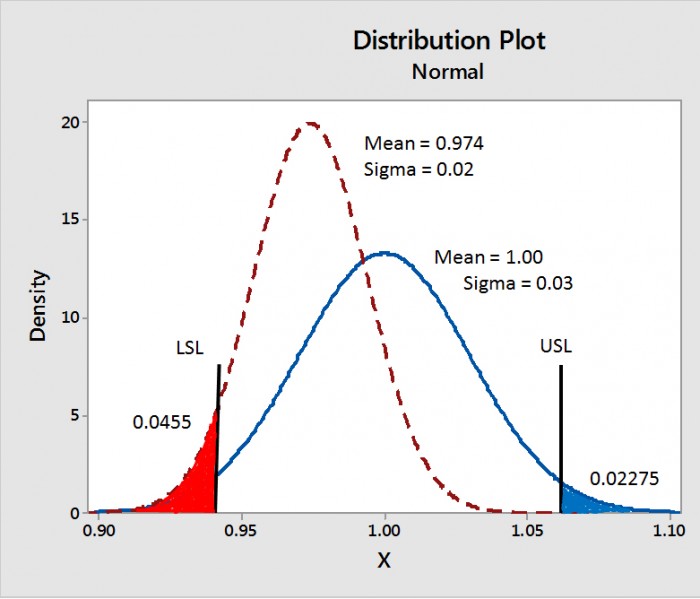
Illustration : Le PowerPoint que Pete avait envoyé à Mike. Remarque : pour la distribution décentrée, tous les défauts sont en dessous de la limite inférieure de spécification. Considérant que, pour la distribution centrée, les défauts sont égaux des deux côtés de la limite des spécifications. Les défauts au total sont les mêmes pour les deux distributions.

« Donc, l'une des courbes a le bon sigma de 0,02 mm, mais elle est décentrée », commenta Mike.

Il fit une pause puis ajouta : « Et l'autre courbe est centrée, mais a un sigma plus élevé de 0,03 mm. »

« Remarquez que tous les défauts sur la courbe excentrée sont sur la partie basse des spécifications ou de limite inférieure de spécification en rouge. Alors que les défauts sur la courbe centrée sont des deux côtés », poursuivit Pete.

« Oui. Et je parie que la courbe décentrée est pire, même si le sigma est plus faible », ajouta Mike.
« Ouais. Le taux de défaillances pour les deux est 0,0455. Mais, la courbe excentrée est pire dans une situation de fabrication », répondit Pete.
« Mais, pourquoi en est-il ainsi, si le taux de défaillances est le même ? » demanda Mike.
« Eh bien, des arbres doivent aller dans ces alésages. Disons que les arbres ont un diamètre moyen de 0,92 mm +/- 0,06. La plupart des analyses de tolérance supposent une distribution centrée. La distribution décentrée des alésages aura 2,8 % d'ajustement avec serrage alors que la distribution centrée aura seulement 1,3 % d'ajustement avec serrage, même si le sigma est de 0,03 mm pour cette distribution », élabora Pete.
« Donc, empiler tous les défauts à une extrémité peut poser un problème ? Laissez-moi deviner que le Cpk pour la distribution centrée est meilleur », Mike répondit.
« Oui. Le Cpk pour la distribution centrée est de 0,667 et pour la distribution de décentré il est de 0,565. Le Cpk donne vraiment la meilleure information sur les données », conclut Pete.
« Comment avez-vous calculé l'ajustement avec serrage ? » demanda Mike.
« Une autre feuille de calcul Excel », rit Pete.
« Ainsi, le résultat net, c'est que le Cpk est roi, non ? » demanda Mike.
« Exactenment », agréa Pete.

Épilogue :

Patty a aidé Pete à préparer sa conférence pour la classe de statistiques, qui comprenait un essai à sec. La conférence de Pete fut un grand succès, et bien qu'il fût nerveux au début, il s'est rapidement détendu.

Merci,

Docteur Ron