電子製造業結論，Cpk =1 代表良率每 100萬有 66,800 缺陷嗎？

Patty、Rob 和 Pete 非常確定他們了解 Cpk = 1 問題的迷惑，但仍想與教授確認。與他寒暄幾句後，他們從教授辦公室致電 ACME 總裁 Mike Madigan。

「教授，很高興再次與您對談，」Madigan 開始說。

大家彼此寒暄，教授感謝 Madigan 透過 ACME 公司資金支持常春藤大學。幾分鐘後，話題回到 Cpk = 1 的問題。.

「天才們告訴我你們的發現吧，」Mike 笑著說。

「我們都想到供應商提供的一篇討論有關統計製程管控 (SPC) 的文章」，Patty 開始說。

「我們特別喜歡製程「控制」和「所能達到」差別的討論，」Rob 接著說。

「但是，66,800 ppm 等同於 3 標準差製程呢？」Mike 懇求地說。

「就我們所知，是 Motorola 開始「六標準差」行動，」教授開始說。「他們定義「六標準差」品質可以為 Cp=2，Cpk=1.5。真正數學的六標準差是 Cp=Cpk=2。他們的定義中 Cpk = 1.5 允許平均 1.5 標準差的位移。常聽到的「六標準差」等於 3.4 ppm 的缺陷就是從這定義而來。由於這個位移，許多的缺陷是分布在同一邊。對了，真正數學的六標準差是每 10億 中有 2 個缺陷，」他繼續說。

「對我來說，這看起來有點作弊，」Madigan 說。

「我也認為如此。我認為他們想要一個東西聽起來吸引人像是「六標準差」，但明知他們無法達成少於 2 ppb 的缺陷，所以他們創造了平均位移 1.5 標準差」Pete 接著說。

「我確信其他人認同 Pete 的說法，但卻是世界上大家所指的「六標準差」。不幸的是它會造成混淆 – 如同手上的案例，」教授回答。

「那怎麼會與每 100萬 有 66,800 個缺陷等於 Cpk=1 及 3 標準差製程相關？」Mike 問。

「Pete 有針對此作出研究。讓他回答吧，」教授建議。

「若你採用平均 1.5 標準差位移至製程能力，可以得到以下表格，」Pete 說。

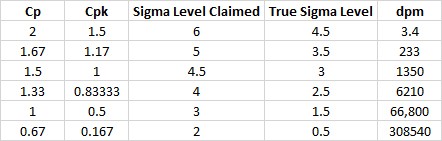
請注意 66,800 dpm 的 Cpk 等級是 0.5 而不是 1，且真正的製程等級不是 3 標準差而是 1.5 標準差。當然 Cp 等級可以是 1，但 Cpk 是個精確的計算，且論文上的圖（參考如下）是錯誤的。它列出的 Cpk 值其實是 Cp 值。這是你的供應商使用此表所犯的錯誤。」Pete 說。

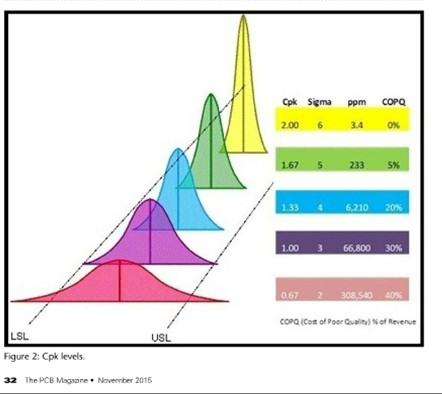
「下圖顯示供應商的情形。分布 A 具有 Cp=Cpk=1，分布 B 則是 Cp=1 但 Cpk 只有 0.5。同時也顯示 B 位移的 1.5 標準差。供應商的數據 66,800 dpm 較接近 B。很重要的一點是Cp 本身並不代表缺陷等級」Pete 繼續說。

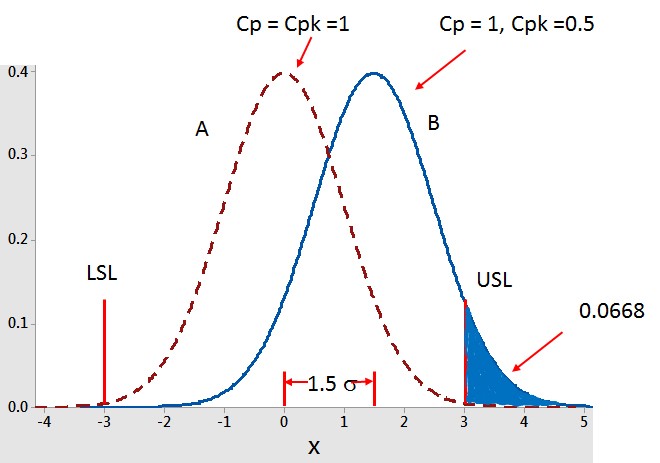
「Pete，請告訴 Mike 你所做的試算表」Patty 建議。

他們都己登錄至 Webex®，於是 Pete 給了一個限制示範。

「輸入規格限值及平均和標準差值後，它可算出 Cp、Cpk、製程標準差限值及製程 dpm」Pete 說。

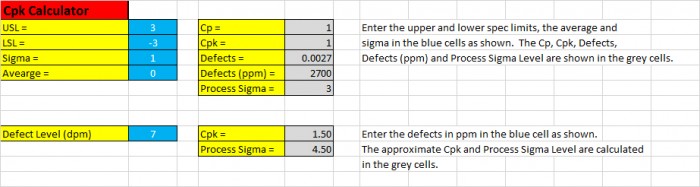
「你也可以輸入 dpm，它會估算出 Cpk 和製程標準差等級」Pete 繼續說。

「相當令人印象深刻，」Madigan 總結。「我想我的團隊應該可以使用它？」他繼續說。

「當然，」Pete 沾沾自喜地說。

數學從不是 Pete 的強項。但在常春藤大學，他最近修了統計學和微積分的課。他對於建立出這個有用的試算表很有成就感。

若您想索取 Pete 的試算表，請寄電子郵件至 rlasky@indium.com。

敬祝，

Dr. Ron