Conclusion de : la fabrication en électronique, Un Cpk = 1 donne-t-il 66,800 défaillances par million ?

Patty, Rob, et Pete étaient tout à fait certains qu'ils comprenaient la confusion dans le problème du Cpk = 1, mais ils tenaient à en discuter avec le professeur. Après une brève conversation avec lui, ils appelèrent Mike Madigan, le PDG d'ACME depuis le bureau du professeur.

" Professeur, c'est toujours un plaisir de parler avec vous," commença Madigan.

Ils échangèrent ensemble quelques plaisanteries et le professeur remercia Madigan pour le soutien financier d'ACME à l'Ivy League. Après quelques instants, la discussion porta sur le problème du Cpk = 1.

" Dites-moi ce que vous, intellectuels géniaux, avez compris," Mike dit en riant.

" Nous avons tous pensé que l'article auquel le fournisseur faisait référence était un grand débat sur la maitrise statistique des procédés (MSP) ”, commença Patty.

" Nous avons particulièrement apprécié la discussion sur la différence entre un procédé en phase de 'contrôle' et un procédé 'capable' ", ajouta Rob.

" Mais, qu'en est-il du fait que 66.800 ppm correspondent à un procédé de niveau Trois Sigma ? " Implora Mike.

" Comme nous le savons, Motorola a lancé le mouvement 'Six Sigma' ", commença le professeur. " Ils définissent la qualité 'Six Sigma' comme ayant un CP de 2 et un Cpk de 1,5. Du point de vue purement mathématique, un niveau Six Sigma correspond à Cp=Cpk=2. Leur définition, avec un Cpk = 1,5, permet un décalage de la moyenne de 1,5 Sigma. L'adage selon lequel 'Six Sigma' correspond à 3,4 ppm défaillances provient de cette définition. En raison de ce décalage, la plupart des défaillances se situent sur un seul côté de la distribution. Par ailleurs, le calcul purement mathématique Six Sigma correspond à 2 défaillances par milliard ", poursuivit-il.

" Cela ressemble un peu à de la tricherie pour moi ", ajouta Madigan.

" Moi aussi. Je pense qu'ils voulaient quelque chose qui sonne sexy, comme 'Six Sigma', mais ils savaient qu'ils ne pouvaient pas vraiment atteindre moins de 2 ppm défaillances, alors ils ont créé le décalage de 1,5 sigma de la moyenne, " renchérit Pete.

" Je suis sûr que d'autres sont d'accord avec Pete, mais c'est là où se situe le monde des 'Six Sigma'. Malheureusement, cela peut prêter à confusion - comme dans notre cas d'espèce, " répondit le Professeur.

" Alors, comment est-ce relié aux 66.800 défaillances par million avec un Cpk de 1 et un procédé Trois Sigma ? " demanda Mike.

" Pete a travaillé largement sur ce sujet. Laissons-le répondre, " suggéra le Professeur.

" Si vous appliquez le décalage de 1,5 Sigma de la moyenne aux capacités des procédés, nous obtenons le tableau ci-dessous," déclara Pete.

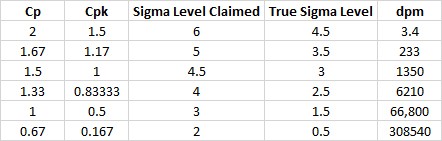
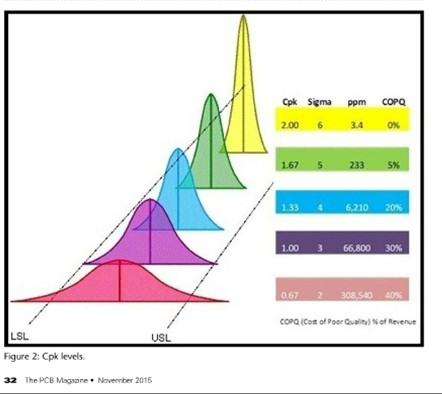
Remarquez que le niveau Cpk pour 66.800 défaillances par million est 0,5 et non 1 et que le véritable niveau du procédé n'est pas Trois Sigma, mais 1,5 Sigma. Certes le niveau Cp serait 1, mais le calcul de Cpk est précis et le graphique issu de l'article en question (reproduit ci-dessous) a tort. Les valeurs qu'ils listent pour Cpk sont les valeurs de Cp. C'est l'erreur faite par votre vendeur à partir de ce graphique. " déclara Pete.

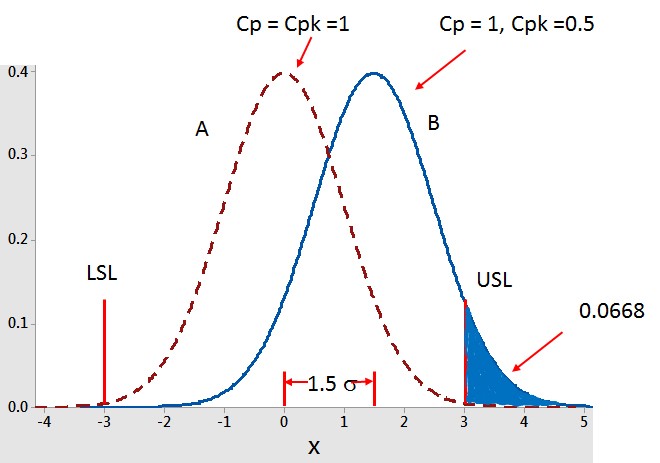
" Le graphique ci-dessous montre la situation pour le vendeur. La distribution A a un Cp et un Cpk = 1, alors que la distribution B a un Cp = 1, mais un Cpk de 0,5 seulement. Le graphique montre aussi le décalage Sigma 1,5 pour la distribution B. Les données du vendeur sont analogues à B, avec les 66.800 défaillances par million. Il est important de noter que Cp seul ne dit rien sur le niveau des défaillances, " continua Pete.

" Pete, voulez-vous parler à Mike de la feuille de calcul que vous avez faite ", suggéra Patty.

Ils étaient connectés à WebEx®, alors Pete donna une démonstration aux limites.

" En entrant les limites des spécifications, ainsi que la moyenne et l’écart type des données, on va calculer Cp, Cpk, la limite de sigma du procédé et le nombre de défaillances par million pour ce procédé ", déclara Pete.

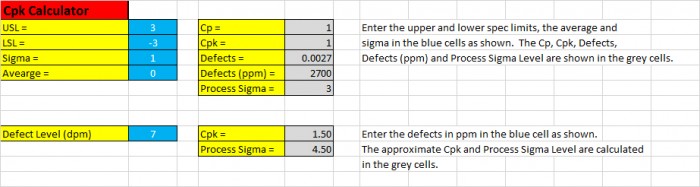
" Oh, et vous pouvez entrer le nombre de défaillances par million et il va estimer le Cpk et le niveau de sigma du procédé, " poursuivit Pete.

" Très impressionnant ", résuma Madigan. "Je suppose que c'est d'accord si mon équipe l'utilise. " continua-t-il.

" Bien sûr ", déclara Pete, rayonnant un peu.

Les maths n'ont jamais été le point fort de Pete. Mais, étant à l'Ivy League, il avait récemment suivi un cours de statistiques et de calcul. Il éprouvait un fort sentiment d'accomplissement après avoir créé cette feuille de calcul bien utile.

Pour ceux qui voudraient une copie de la feuille de calcul de Pete, envoyez-moi un courriel à rlasky@indium.com.

Merci,

Docteur Ron