电子制造业总结，Cpk =1 是否允许每 100 万个产品中有 66,800 个不合格品？

Patty、Rob 和 Pete 很肯定他们了解 Cpk = 1 问题的混乱所在，但还是想和教授一起讨论下。与教授简短交流后，他们在教授的办公室拨通了 ACME 首席执行官 Mike Madigan 的电话。

“教授，您好！很高兴再次和您通话。”Madigan 开口道。

他们相互寒暄，教授感谢 Madigan 通过 ACME 公司给予常春藤大学的资金支持。片刻之后，话题转向了 CPK=1 问题。

“告诉我，你们这些聪明的家伙弄清楚了些什么？” Mike 笑道。

“我们都认为那个供应商所参考的文章关于统计流程控制（SPC）的探讨非常棒。” Patty 开始道。

“我们特别喜欢关于 ‘流程控制’ 和 ‘流程能力’ 之间差异的讨论。” Rob补充道。

“但是，66,800 ppm 等同于三西格玛流程是怎么回事？”Mike 恳切的问道。   

“据我们所知，是摩托罗拉开始了‘六西格玛’运动。”教授开始道。“他们将‘六西格玛’的质量水平定义为 Cp=2，Cpk=1.5。而真正数学上的六西格玛是 Cp=Cpk=2。根据他们的定义，Cpk=1.5，允许均值 1.5 西格玛的偏移。而‘六西格玛’允许有 3.4 ppm 缺陷率的宣称就来自于该定义。由于这一偏移，大部分的缺陷位于分布图的一侧。顺便说一下，数学上的六西格玛允许每 10 亿个产品中仅有两个缺陷产品。”他继续道。 

“看起来有点像他们欺骗了我。”Madigan 补充道。

“我也这么认为。我想他们大概是想让产品听起来更炫一点吧，比如符合‘六西格玛’标准，但又知道他们无法真正实现缺陷率低于 2 ppb，所以他们创造了均值 1.5 西格玛的偏移。” Pete 说道。

“我肯定其他人也同意 Pete 的意见，但这就是‘六西格玛’的世界。不幸的是，这就产生了混乱——如同我们碰到的这个例子一样。”教授回答道。

“那么这与每一百万个产品允许 66,800 个缺陷产品等同于 Cpk=1 和三西格玛流程有什么关系？”Mike 问道。

“Pete 对这个比较有研究。我们让他来回答。”教授建议道。

“如果你在过程能力中应用了均值 1.5 西格玛偏移，我们就能得到如下表格。” Pete 说道。

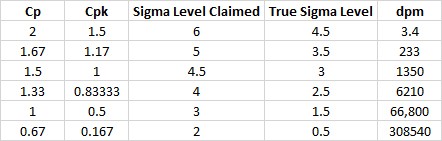
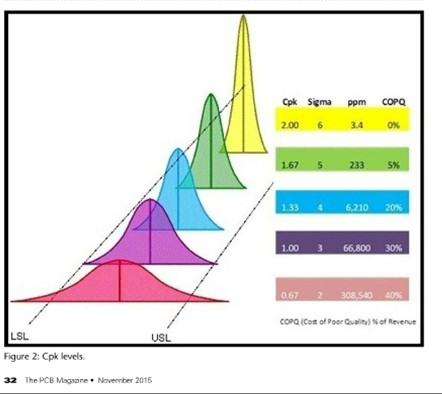
“请注意 66,800 dpm 缺陷率的 Cpk 水平是 0.5 而不是 1 ，所以真正的流程水平不是三西格玛，而是 1.5 西格玛。诚然Cp =1，但是 Cpk 是一种精确的计算，而文章里所涉图表（见如下复制图）中这个值是错误的。他们所列出的 Cpk 的值是 Cp 的值。这就是你的供应商使用这个表格所犯的错误。”Pete 说道。

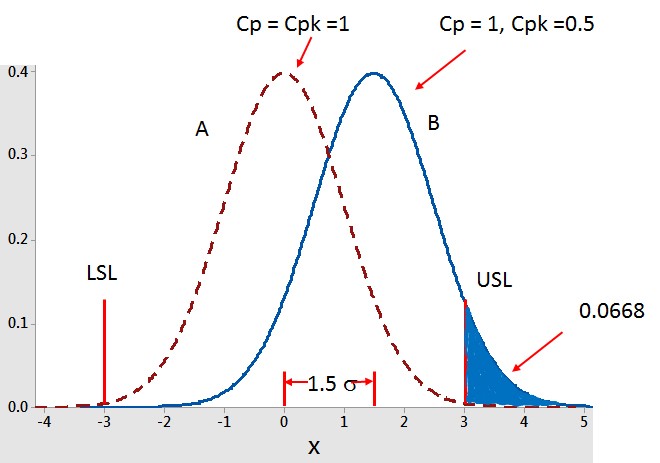
“这个表格显示的就是供应商的情况。分布图 A 中 Cp 和 Cpk =1，分布图 B 中 Cp=1， 但是 Cpk 仅为 0.5 。图表中也显示了分布图B中的 1.5 西格玛偏移。供应商的数据类似于分布图B，缺陷率为66,800dpm……需要重点强调的是单 Cp 值并不能说明缺陷水平如何。” Pete 继续说道。

“Pete，请继续给 Mike 讲讲你制作的电子表格。”Patty 建议道。

他们登录 Webex®， Pete 进行了有限的演示。

“输入标准限值以及数据的均值和西格玛，就可以计算出 Cp、CPk、流程的西格玛限制以及流程 dpm。”Pete 说道。

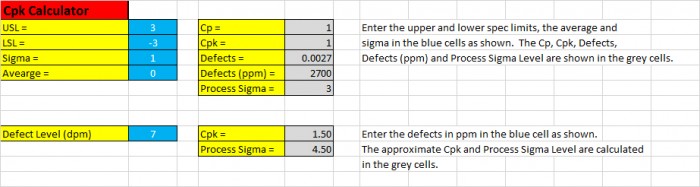
“哦，你可以输入 dpm， 它将估量 Cpk 和流程的西格玛水平。”Pete 继续道。

“非常不错，令人印象深刻。”Madigan 总结道。“如果我的团队使用这个应该没问题吧？”他继续说。

“当然。” Pete 高兴地说。

数学从来不是 Pete 的强项。但是，他最近在常春藤大学进修统计和微积分学课程。创建一个有帮助的电子表格让他有很强的成就感。

如果您想要一份 Pete 的电子表格副本，请发邮件到 rlasky@indium.com 索取。

谢谢，

Ron 博士