Fazit der In elektronischen Herstellung, ergibt Cpk =1 66.800 Fehler je Million?

Patty, Rob, und Pete waren ganz sicher, dass sie die Verwirrung beim Cpk = 1 Problem verstanden hatten, aber wollten sichergehen, es mit dem Professor zu diskutieren. Nach einem kurzen Gespräch mit ihm, riefen sie ACMEs CEO Mike Madigan vom Büro des Professors aus an.

„Professor, es ist toll, wieder mit Ihnen zu sprechen“, begann Madigan.

Sie alle tauschten Höflichkeiten aus, wobei der Professor Madigan für seine finanzielle Unterstützung der Eliteuniversität durch die ACME Corporation dankte. Nach wenigen Augenblicken kam die Diskussion auf das Cpk = 1 Problem.

„Sagen Sie mir, was Sie erstaunliche Intellektuelle herausgefunden haben," lachte Mike.

„Wir dachten alle dass der Artikel, auf den sich der Anbieter bezog, bei der statistischen Verfahrenkontrolle (SPC) stark diskutiert wurde", begann Patty.

„Besonders gut gefallen hat uns die Diskussion über den Unterschied zwischen einem Verfahren, das  „führt“ und einem, das „funktioniert““, fügte Rob hinzu.

„Aber was ist mit den 66,800 ppm, die einem Drei Sigma-Verfahren entsprechen?" fragte Mike eindringlich.   

„Wie wir wissen, startete Motorola die „Six Sigma'-Bewegung", begann der Professor. „Sie definierten die „Six Sigma' -Qualität  mit einem Cp von 2 und einem Cpk von 1,5.  Das wahre mathematische Six Sigma ist Cp=Cpk=2.  Ihre Definition mit einem Cpk = 1,5 bringt eine Verschiebung des Mittelwertes von 1,5 Sigma.  Die Faustregel  „Six Sigma' gleich 3,4 ppm Fehler kommt von dieser Definition.  Aufgrund dieser Verschiebung befinden sich die meisten Fehler auf der einen Seite der Streuung. Übrigens,das wahre mathematische Six Sigma ist ca. 2 Fehler pro Milliarde", fuhr er fort.

„Es scheint mir ein wenig wie Betrug zu sein," fügte Madigan hinzu.

„Mir auch. Ich glaube, sie wollten etwas sexy klingen, wie „Six Sigma', aber sie konnten nicht wirklich weniger als 2 ppb Fehler erzielen, daher schufen sie die 1,5 Sigma -Verschiebung des Mittelwertes", fiel Pete ein.

„Ich bin sicher, dass andere Pete zustimmen, aber das ist die Welt von „Sechs Sigma'.  Leider kann das Verwirrung stiften - wie im vorliegenden Fall", antwortete der Professor.

„Wie bezieht sich das sich auf die 66.800 Fehler pro Million, die einem Cpk von 1 und einem Drei  Sigma-Verfahren entsprechen?" fragte Mike .

„Pete hat am meisten daran gearbeitet.  Lassen wir ihn das beantworten", schlug der Professor vor.

„Wenn Sie die 1.5 Sigma -Verschiebung des Mittelwertes auf die Verfahrensfähigkeiten anwenden, erhalten wir die folgende Tabelle", sagte Pete. 

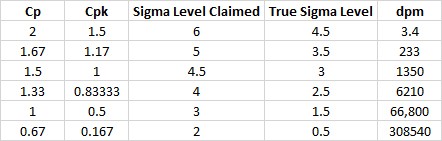
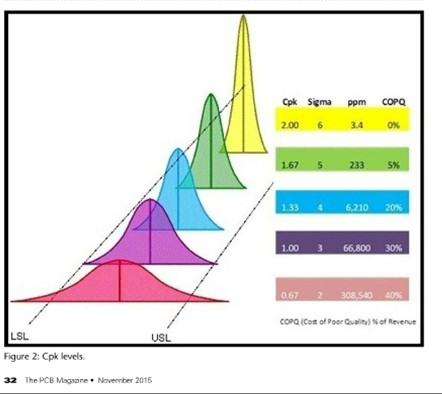
Beachten Sie, dass der Cpk-Wert für 66.800 dpm  0,5 und nicht 1 und das wahre Verfahrenniveau nicht Three Sigma, sondern 1,5 Sigma ist. Zugegeben, das CP-Niveau könnte 1 sein, aber Cpk ist eine genaue Berechnung, und die Grafik aus dem betreffenden Aufsatz (abgedruckt unten) ist falsch. Die Werte, die sie für Cpk aufführen sind die Cp-Werte.  Dieses ist der Fehler, den Ihr Anbieter anhand dieserTabelle macht. " sagte Pete.

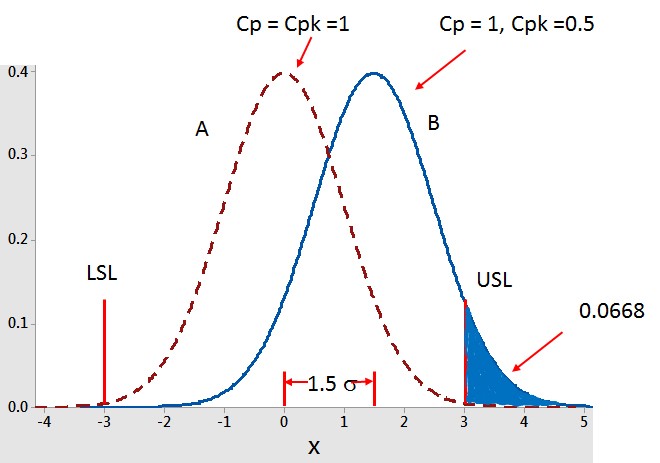
„Die Grafik unten zeigt die Situation für den Anbieter.  Streuung A hat einen Cp und Cpk =1, wohingegen Streuung B einen Cp = 1, aber einen Cpk von nur 0,5 hat. Die Verschiebung von 1,5 Sigma  für B wird ebenfalls angezeigt.  Die  Daten des Anbieters sind ähnlich wie B, mit seinen 66.800 dpm..Man muss beachten, dass Cp allein  nichts über die Fehlergröße aussagt ", fuhr Pete fort.

„Pete, informiere bitte Mike über die Tabellenkalkulation, die du erstellt hast", schlug Patty vor.

Sie loggten sich bei Webex® ein und  Pete gab eine Demonstration der Grenzen. 

„Durch Eingabe der Spezifikationsgrenzen sowie des Mittelwertes und Sigma der Daten, wird das Cp, Cpk, die Sigma -Grenze des Verfahrens und der Verfahrens- dpm berechnet", sagte Pete.

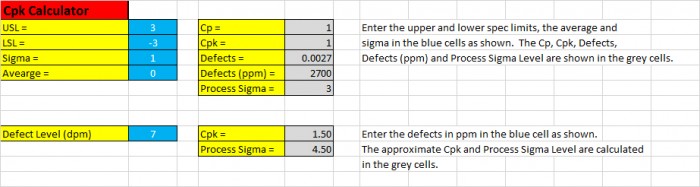
„Oh, und  Sie können den dpm eingeben und das Cpk und das Niveau des Sigma-Verfahrens wird geschätzt ", fuhr Pete fort.

„Sehr beeindruckend", fasste Madigan  zusammen. „Ich nehme an, es ist in Ordnung, wenn mein Team sie nutzt?", fuhr er fort.

„Sicher", sagte Pete und strahlte ein wenig.

Mathematik war nie Petes Stärke. Aber an der Eliteuniversität  hatte er  vor Kurzem einen Statistik- und Rechenkurs belegt. Er war nach der Erstellung dieser nützlichen Tabelle sehr zufrieden.

Diejenigen, die eine Kopie von Petes Tabellenkalkulation erhalten möchten, senden Sie mir eine E-Mail an rlasky@indium.com.

Danke,

Dr. Ron