政治性民調的誤差範圍

各位，

今年我們很多人都非常關注總統選舉。有些人可能不了解每天討論民調數據中的「誤差範圍」是什麼意思。

民調的統計數據是以二項式分布說明。這個分布的開發目的是用以說明是/否、正面/反面、對/錯、候選人A/候選人B等。兩者任一的數據性質稱為伯努利試驗。

舉例而言，假設你擲公平的硬幣1,000次。最有可能是正面的次數為500次，但若數據為492或507次也不會覺得奇怪。但若正面的次數是200次就會感到驚訝。下圖顯示這種情形的二項式分布。

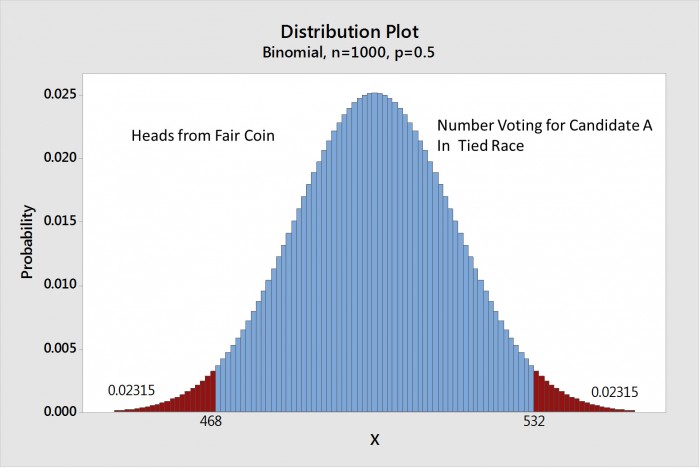
圖：擲硬幣1,000次的結果，正面介於468次至532次的機率約為95%。

低於468次和高於532次的區域標示為紅色，在這些區域的統計顯著性得到正面低於468次和高於532次的機率只有5%。但其具有四捨五入的小誤差，實際機率是略低於5%的4.63%。

因此，你擲硬幣1,000次會有約95%的機率得到介於468和532之間的正面次數。   全球已將此“95%”作為統計顯著性的標準。也就是擲硬幣1,000次會有95%的機率得到正面的次數並以+/- 3.2%（高於32或低於500除以1,000）改變。+/- 3.2%就是所謂的「誤差範圍」，又稱為MOE。

現在讓我們將此應用在總統選舉的民調。民調人員竭盡所能地對代表全國的樣本人數做民意調查。。這不是個簡單的任務。但假設他們取得公平的樣本，即便像是各50:50機率的比賽，如擲硬幣，也不見得取得各50:50的樣本數。結果會如同擲硬幣，即便是50:50的比賽中，會有95%的機率得到次數介於468至532之間。

大多數的民調顯示MOE約為3%，因此我們可得知取樣數為約1,000。

敬祝，

Dr. Ron