政治民意调查中的误差幅度

各位，

我们当中很多人都被今年的总统选举吸引住了。有些人可能也会对每天讨论的民意调查数据中所谓的“误差幅度”的含义表示不解。

民意调查统计是通过二项分布描述的。二项分布是为了描述数据的是/否、正/反、真/假以及候选人 A/候选人 B等。数据的这种非此即彼的本质就是所谓的伯努利试验。

举例而言，让我们假设你抛掷了一枚硬币 1,000次。最有可能的是你得到 500 次正面，但是如果得到 492 或 507 次正面，相信你也不会感到惊讶。但是如果你仅仅获得 200 次正面，那么你肯定会感到意外了。下图将展示这种情形的二项分布。

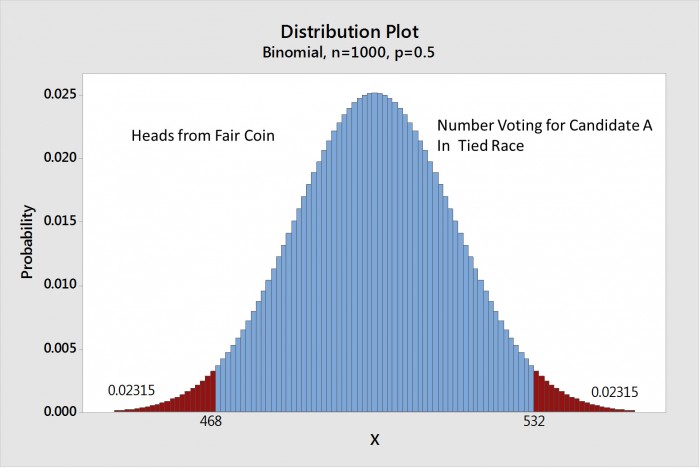
图：在大约95%的情况下，抛掷一枚硬币 1,000次，获得正面的次数在 468 至532 次之间。

请注意468 次以下或532 次以上的区域是红色的，这些区域具有显著的统计学意义，因为你获得正面的次数低于468 或者高于532 的几率仅为 5% 。其实这里还存在一个舍入误差，真正的确切数字是 4.63 %，略低于 5%。

所以，当你抛掷一枚硬币 1,000次，在约 95% 的情况下，获得正面的次数在 468 至532 次之间。   在这里，将这个“95%”设定为统计学意义的标准。所以，当你抛掷 1,000次时，在 95% 的情形下，正面的次数将围绕 +/- 3.2% 变化（将 1,000 次平分，比 500 次高 32 次或低 32 次之间）。这里的 +/- 3.2% 便是“误差幅度”，也可以用 MOE 表示。

现在让我们来看看总统选举中的民意调查。民意调查专家尽力地获取代表这个国家的人民意见的调查样本。这并不是一件轻松的事。但是，假设他们获得了一个适当的样本，即使在 50/50 的比赛中，就像抛掷硬币一样，他们也不一定能获得一个50/50 的样本。就如同抛掷硬币一样，在95% 的情况下，他们所获得的结果在 468 至 532 之间，哪怕是在50/50 的比赛中也是的。

大多数民意调查显示，误差幅度（MOE）为 3%，所以我们知道样本规模约为 1,000。

谢谢，

Ron 博士