Marge d'erreur dans les sondages politiques

Les amis,

Nombre d'entre nous sont fascinés par l'élection présidentielle cette année. Certains peuvent se demander ce que signifie la « marge d'erreur » dans les résultats des sondages dont on parle quotidiennement.

La distribution statistique d'un sondage est décrite par la distribution binomiale. Cette distribution a été élaborée pour décrire des données comme oui/non, pile/face, vrai/faux, candidat A/candidat B, etc. La nature des résultats, succès/échec est ce qu'on appelle une épreuve de Bernoulli.

À titre d'exemple, supposons que vous lanciez une pièce de monnaie équilibrée 1 000 fois. Le nombre de fois où le résultat sera face est de l’ordre de 500, mais vous ne seriez pas surpris si vous obteniez 492 ou 507 fois face. Vous seriez certainement surpris si vous obteniez seulement 200 face. La figure ci-dessous montre la distribution binomiale pour cette situation.

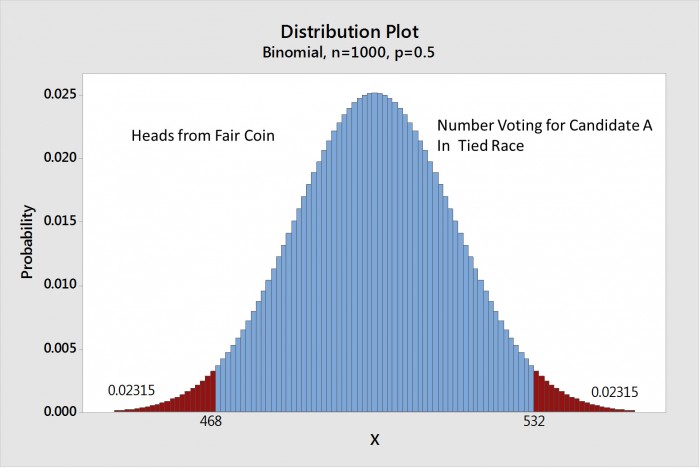
Figure : Dans environ 95 % des cas, le lancer 1 000 fois d'une pièce de monnaie équilibrée entraînera entre 468 et 532 de face.​

Remarquez les surfaces en rouge en-dessous de 468 ou au-dessus de 532. Ces zones signifient en statistiques qu'il n'y a qu'une chance de 5 % que vous obteniez un résultat situé soit en-dessous de 468, soit au-dessus de 532 fois face. Il y a une petite erreur d'arrondi, ainsi le nombre réel est 4,63 %, soit un peu moins de 5 %.

Ainsi, dans environ 95 % des cas, si vous lancez 1 000 fois une pièce de monnaie, le nombre de face sera compris entre 468 et 532. La communauté a défini ce « 95 % » comme le critère de signification statistique. Ainsi, le nombre de face variera de +/- 3,2 % (32 au-dessus ou au-dessous de 500, divisé par 1 000) dans 95 % des cas où vous effectuez les 1 000 lancers. Ce +/- 3,2 % est appelé la « marge d'erreur ».

Maintenant, nous allons adapter ceci aux sondages sur l'élection présidentielle. Les sondeurs s'efforcent d'interroger un échantillon de personnes caractéristique de la nation. Ce n'est pas une mince affaire. Cependant, en supposant qu'ils travaillent sur un échantillon équilibré, même dans une course à la présidentielle à 50/50, tout comme pour le lancer d'une pièce de monnaie, ils n'obtiendront pas nécessairement un échantillon avec un résultat de 50/50. Leurs résultats seront tout comme dans le cas du lancer d'une pièce de monnaie, ils auront dans 95 % des résultats 468-532, même dans une course à 50/50.

La plupart des sondages montrent une marge d'erreur d'environ 3 %, donc nous savons que la taille de l'échantillon est d'environ 1 000.

Merci,

Docteur Ron