Équation de la densité d'un alliage de soudure : Pourquoi ce que la plupart des gens considèrent comme juste est faux

Les amis,

C'est difficile à croire, mais je blogue depuis plus de 10 ans. Pendant tout ce temps, parmi les centaines d'articles que j'ai postés, le sujet le plus populaire a été de loin le calcul de la densité d'un alliage métallique.  Une des raisons de cette popularité, c'est de croire que la densité d'un alliage est déterminée par l'équation :

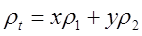   eq. 1

Où x est la fraction de la masse du métal 1, y la fraction de la masse du métal 2, ρ les densités respectives et ρ_t la densité totale de l'alliage.   J'ai montré dans le passé que la formule correcte pour calculer la densité d'un tel alliage est :

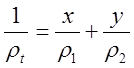     eq. 2

Cette formule est à nouveau démontrée ci-dessous.

qui a été peu utile.  J'ai utilisé un exemple qui démontre que l'équation 1 est fausse et j'ai obtenu ensuite une explication qui a été peu utile.  J'ai utilisé un exemple qui démontre que l'équation 1 est fausse et j'ai obtenu ensuite une équation ressemblant à l'équation 1 mais utilisant les fractions volumiques au lieu des fractions massiques.  La démonstration figure ci-dessous et l'équation est la suivante :   

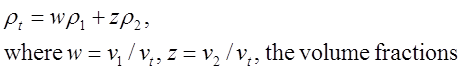                    eq. 3

Toutefois, l'équation 3 n'est pas très utile car la fraction volumique de chaque métal n'est pas aussi facilement connue que la fraction massique, qu'il est facile de mesurer à l'aide d'une balance.

Maintenant, pour donner un exemple qui prouve que l'équation 1 n'est pas raisonnable, imaginons une expérience qui va démontrer que l'équation 1 est loin d'être juste.  Considérons un mètre cube d'air dans un récipient de 1 mètre de côté à la température ambiante.  Le mètre cube d'air va peser 1,225 kg. (Le fait que l'air soit si lourd surprend beaucoup de gens...).  À l'intérieur du récipient se trouve 1,225 kg d'une poudre d'or fine. Nous mélangeons la poudre d'or dans l'air de sorte qu'elle occupe la totalité du récipient avec une concentration homogène.  La poudre est si fine qu'elle va demeurer suspendue pendant une période assez courte.  Nous pourrons donc considérer ce mélange comme un alliage d'or et d'air.  Les fractions massiques x et y sont égales à 0,50.  Si l'équation 1 était juste, la densité de « l'alliage » devrait être :

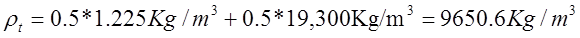
Figure 1. Expérience sur la densité d'un mélange d'or et d'air

La masse du récipient d'un mètre cube serait dans ce cas 9650,6 kg/m³ x 1 m³ = 9650,6 kg !  Mais nous savons qu'elle est de 1,225 kg + 1,225 kg = 2,45 kg. L'équation 2 ou l'équation 3 fournit la réponse correcte.

Voici les calculs corrects :

Merci,

Docteur Ron