스텐실 인쇄 전달 효율 Cpk용 가설 테스트 스프레드시트

여러분,

모든 SMT 불량 중 2/3 가 스텐실 인쇄 공정으로 거슬러 올라갈 수 있다는 것을 모든 사람이 사실로 인정하고 있어요. 우리 중 상당수는 이 사실로 받아들이는 것에 대한 참조를 찾으려 노력했으나 성공하지는 못했어요. 독자분들 중 아시는 분이 계시다면 저에게 알려주세요. 이 격언이 사실이라고 가정하면 패드에 정사각형으로 인쇄된 올바른 양의 솔더 페이스트는 매우 중요한 척도에요.

이러한 관점에서 얼마전에 저는 게시글에서 스텐실 인쇄에서 전달 효율의 Cpk 신뢰 구간 계산에 대한 글을 썼어요. 즉, 전달 효율은 솔더 페이스트 증착물의 부피를 스텐실 개구부의 부피로 나눈 비율이에요. 도표 1을 참조하세요. 일반적으로 목표는 100%이고 상단 및 하단 사양은 각각 150% 및 50%에요.

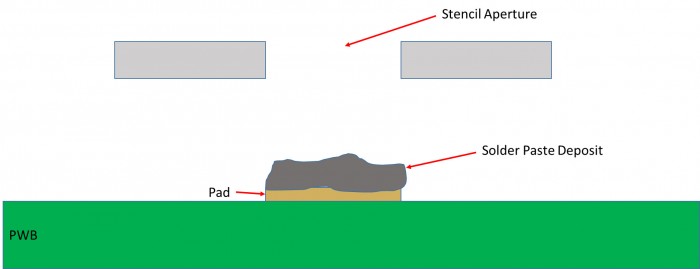
도표 1. 스텐실 인쇄에서 전달 효율은 솔더 페이스트 증착물의 부피를 스텐실 개구부의 부피로 나눈 비율이에요. 일반적인 목표는 100%에요.

저는 평균 및 표준 편차(즉, “분포”) 둘 다 포함되기 때문에 스텐실 인쇄 전달 효율을 평가하기 위한 최고 척도로 Cpk를 선택했어요. 도표 2에서 페이스트 A는 데이터가 사양 사이에 집중된 날카로운 분포를 보여, 훌륭한 Cpk를 가지는 반면, 페이스트 B의 분포는 사양 사이에 집중되지 않고 넓게 분포된 것을 보여줍니다.

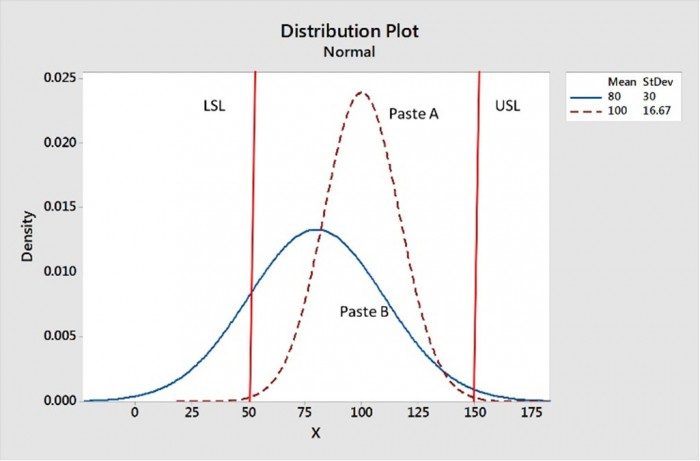
도표 2. 페이스트 A는 상단 및 하단 사양 간에 데이터가 집중된 보다 나은 전달 효율을 보이며 날카롭게 분포되어 있습니다.

최근 저는 Cpk의  가설 테스트를 수행할 수 있는 엑셀 스프레드시트를 만들기 위해 수학을 개발하기로 결정했어요. 제가 아는 한, 이것은 이전에 한 번도 해본 적이 없어요.

가설 테스트는 아래와 같을 겁니다. 귀무 가설 (Ho)은 Cpk 전달 효율이 1.00이 될 수 있어요. 대체 가설 H1은 Cpk가 1.00이 아닐 수 있어요. H1은 또한 1.00보다 작거나 클 수 있어요.

예를 들어 Cpk 전달 효율을 1.00으로 설정한다고 가정해 보기로 해요. 1000개의 인쇄를 분석하여 Cpk 0.98을 얻어요. 모두 손실되었나요? 반드시 필요한 것은 아니지만, 이것은 통계적인 표본이었기 때문에 가설 테스트를 수행해야만 해요. 도표 3을 참조하세요. 셀 B16에 Cpk = 0.98를 입력하고, 셀 B17에 표본 크기 n = 1000을 입력하고, 셀 B18의 귀무 가설: Cpk = 1.00 이 입력되었어요. 셀 B21은 대체 가설이 거짓일 때 거짓으로서 귀무 가설이 거부될 수 없음을 보여주죠. 따라서 우리는 통계적으로 Cpk가 1.00과 같지 않다고 말할 수 없어요.

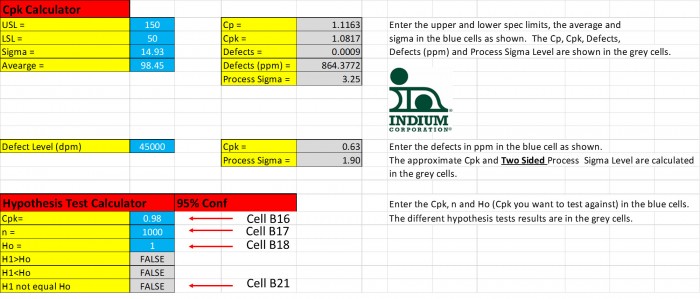
도표 3. 귀무 가설 Ho가 거부될 수 없으므로 Cpk = 0.98은 Cpk 1.00과 통계적으로 같아요.

통계적으로 1.00과 같지 않다고 말하기 위해 이 1000개의 표본의 예에서 Cpk가 1.00과 얼마나 차이가 있을까요? 도표 4는 Cpk가 1.00과 통계적으로 다른 0.95 (또는 1.05)이어야 한다는 것을 나타내요.

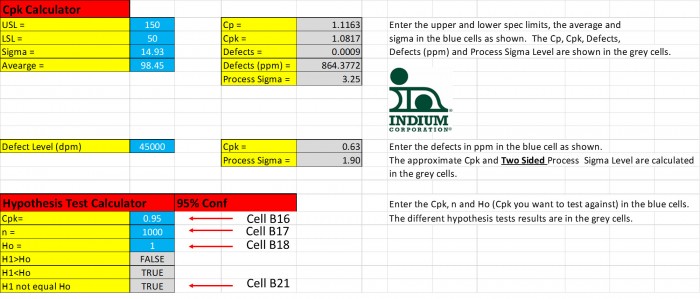
도표 4. Cpk가 단지 0.95인 경우, 이 Cpk는 Cpk = 1.00과 통계적으로 달라요.

이 스프레드시트는 종단 라인 솔더링 불량을 줄이기 위한 전달 효율을 모니터링하는 데 관심이 있는 사람들에게 유용해야 해요. 관심이 있으신 독자분들께 이 스프레드시트 사본을 보내드릴게요. 받으시기 원하시는 경우 저에게 이메일 rlasky@indium.com로 요청해 주세요.

감사합니다,

론 박사