Tabellenkalkulation mit einem Hypothesentest für den CpK-Wert der Transfereffizienz beim Schablonendruck

Leute,

alle, die ich kenne, sehen es als gegeben an, dass ca. zwei Drittel aller SMT-Mängel auf den Schablonendruckprozess zurückzuführen sind. Viele von uns haben versucht, einen Nachweis für diese Aussage zu finden, jedoch ohne Erfolg. Sollte irgendein Leser einen kennen, dann lassen Sie es mich bitte wissen. Vorausgesetzt, diese Aussage ist wahr, dann ist die richtige Menge von Lotpaste, die direkt auf das Pad gedruckt wird, eine äußerst wichtige Messgröße.

Angesichts dessen schrieb ich vor einiger Zeit einen Blogbeitrag über die Berechnung des Konfidenzintervalls des CpK-Werts der Transfereffizienz beim Schablonendruck. Zur Erinnerung: Die Transfereffizienz ist das Verhältnis des Volumens des Lotpastendepots geteilt durch das Volumen der Schablonen-Aperture. Siehe Abbildung 1. Das Ziel wäre normalerweise 100 % mit oberen und unteren Grenzwerten bei jeweils 150 % bzw. 50 %.

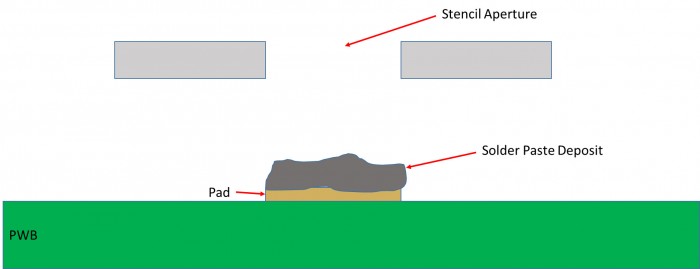
Abbildung 1. Die Transfereffizienz beim Schablonendruck ist das Volumen des Lotpastendepots geteilt durch das Volumen der Schablonen-Aperture. Das Ziel ist normalerweise 100 %.

Ich wählte den CpK-Wert als beste Messgröße zur Bewertung der Transfereffizienz bei Schablonendruck, da er sowohl den Durchschnitt als auch die Standardabweichung (d. h. die „Ausbreitung“) umfasst. Die Abbildung 2 zeigt die Verteilung der Paste A mit einem guten CpK-Wert, da die Daten eng verteilt zwischen den Grenzwerten zentriert sind, während die Verteilung der Paste B nicht zwischen den Grenzwerten zentriert und darüber hinaus breit ist.

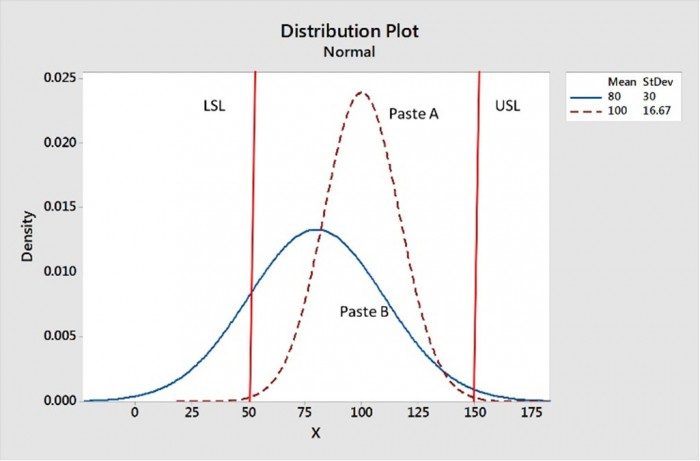
Abbildung 2. Die Paste A weist die bessere Transfereffizienz auf, da die Daten zwischen dem oberen und unteren Grenzwert zentriert und enger verteilt sind.

Vor Kurzem beschloss ich dann, die mathematische Formel zur Erzeugung einer Excel-Tabelle zu entwickeln, die Hypothesentests der CpK-Werte durchführt. Soviel ich weiß, wurde dies noch nie getan.

Ein Hypothesentest sieht in etwa wie folgt aus. Die Nullhypothese (Ho) wäre, dass der CpK-Wert der Transfereffizienz 1,00 beträgt. Die alternative Hypothese H1 könnte sein, dass der CpK-Wert ungleich 1,00 ist. H1 könnte auch sein, dass H1 kleiner oder größer als 1,00 ist.

Lassen Sie uns beispielsweise annehmen, Sie wünschen einen CpK-Wert der Transfereffizienz von 1,00. Sie prüfen 10000 Drucke und erhalten einen CpK-Wert von 0,98. Ist jetzt alles verloren? Nicht unbedingt. Da es sich um eine statistische Stichprobe handelte, sollten Sie einen Hypothesentest durchführen. Siehe Abbildung 3. In das Feld B16 wurde der CpK-Wert = 0,98, in das Feld B17 die Stichprobengröße n = 1000 und in das Feld B18 die Nullhypothese von: CpK-Wert = 1,00 eingegeben. Feld B21 zeigt, dass die Nullhypothese nicht als unwahr abgelehnt werden kann, da die alternative Hypothese unwahr ist. Statistisch kann daher nicht gesagt werden, dass der CpK-Wert ungleich 1,00 ist.

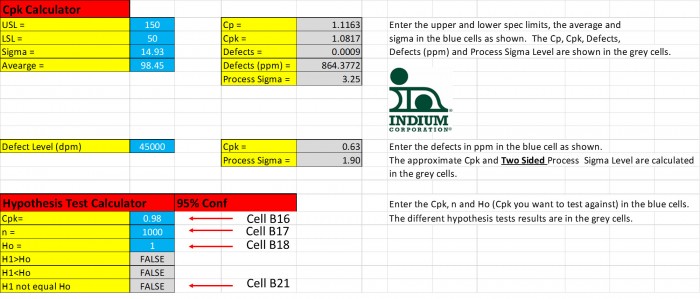
Abbildung 3. Ein Cpk-Wert = 0,98 entspricht statistisch einem CpK-Wert von 1,00, da die Nullhypothese Ho nicht abgelehnt werden kann.

Wie weit müsste der CpK-Wert bei einer Stichprobengröße von 1000 abweichen, um sagen zu können, dass er statistisch ungleich 1,00 ist? Die Abbildung 4 zeigt, dass der CpK-Wert 0,95 (bzw. 1,05) betragen müsste, um statisch von 1,00 abzuweichen.

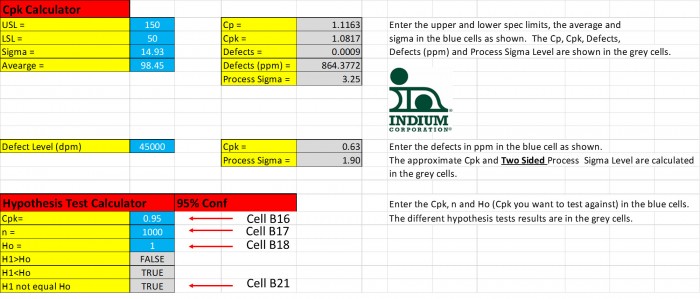
Abbildung 4. Wenn der CpK-Wert lediglich 0,95 beträgt, ist er statistisch ungleich einem CpK-Wert = 1,00.

Diese Tabellenkalkulation sollte für alle hilfreich sein, die CpK-Werte der Transfereffizienz überwachen wollen, um End-of-Line-Lötmängel zu reduzieren. Ich kann interessierten Lesern eine Kopie dieser Tabellenkalkulation senden. Senden Sie Ihre Anfragen dazu einfach an rlasky@indium.com.

Danke,

Dr. Ron