Feuille de calcul de test d'hypothèse pour le Cpk de l'efficacité de transfert de l'impression au pochoir

Les amis,

Tout le monde reconnaît que les 2/3 de tous les défauts des CMS peuvent être retracés jusqu'au processus d'impression au pochoir. Un certain nombre d'entre nous ont essayé de trouver une référence pour ce postulat, sans succès. Si un lecteur en connaît une, merci de me le faire savoir. En supposant que cet adage soit vrai, la bonne quantité de crème à souder, imprimée en carré sur la pastille est une mesure extrêmement importante.

Dans cette perspective, il y a quelque temps, j'ai écrit  un article sur le calcul de l'intervalle de confiance du Cpk de l'efficacité du transfert de l'impression au pochoir. Pour rappel, l'efficacité du transfert est le rapport entre le volume du dépôt de crème à souder divisé par le volume de l'ouverture du pochoir. Voir Figure 1. Généralement, l'objectif est 100 %, les spécifications supérieures et inférieures étant respectivement de 150 % et de 50 %.

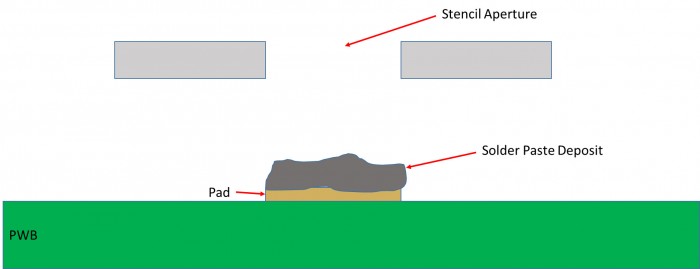
Figure 1. L'efficacité du transfert d'une impression au pochoir est le rapport entre le volume du dépôt de crème à souder divisé par le volume de l'ouverture du pochoir. Généralement, l'objectif est 100 %.

J'ai choisi le Cpk comme la meilleure mesure pour évaluer l'efficacité du transfert d'impression au pochoir car il incorpore à la fois la moyenne et l'écart type (c'est-à-dire la "diffusion"). La figure 2 montre la distribution pour la crème A, qui a un bon Cpk car ses données sont centrées entre les spécifications et la distribution est étroite, alors que la distribution de la crème B n'est pas centrée entre les spécifications et que sa distribution est étendue.

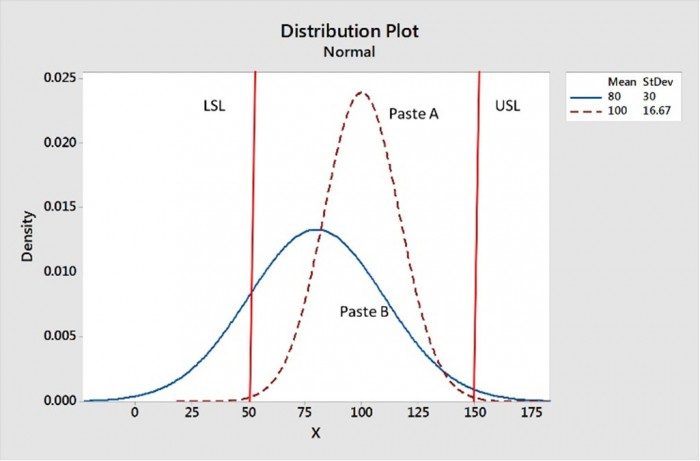
Figure 2. La crème A a la meilleure efficacité de transfert, car ses données sont centrées entre les spécifications supérieures et inférieures, et sa distribution est plus étroite.

Récemment, j'ai décidé de mettre au point les calculs pour produire une feuille Excel qui effectuerait des tests d'hypothèses sur les Cpk. Autant que je sache, cela n'a jamais été fait auparavant.

Un test d'hypothèse pourrait ressembler à ce qui suit. L'hypothèse zéro (Ho) serait que le Cpk de l'efficacité du transfert serait de 1,00. L'hypothèse alternative, H1, serait que le Cpk ne soit pas égal à 1,00. H1 pourrait également être que le Cpk serait inférieur ou supérieur à 1,00

Par exemple, disons que vous voulez que le Cpk de l'efficacité du transfert soit de 1,00. Vous analysez 1000 impressions et obtenez un Cpk de 0,98. Tout est perdu ? Pas nécessairement, puisqu'il s'agissait d'un ​échantillonnage statistique, vous devriez effectuer un test d'hypothèse. Voir Figure 3. Dans la cellule B16, le Cpk = 0,98 a été entré, dans la cellule B17, on a entré la taille de l'échantillon n = 1000 et dans la cellule B18, l'hypothèse zéro : Cpk = 1,00 est entrée. La cellule B21 montre que l'hypothèse zéro ne peut pas être rejetée comme fausse car l'hypothèse alternative est fausse. Nous ne pouvons donc pas dire statistiquement que le Cpk n'est pas égal à 1,00.​

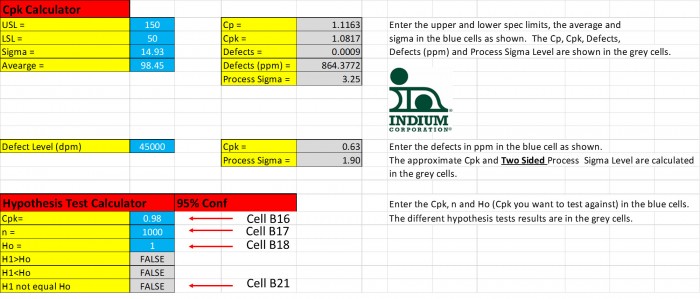
Figure 3. Un Cpk = 0,98 est statistiquement identique à un Cpk de 1,00 car l'hypothèse zéro, Ho, ne peut pas être rejetée.​

À quel point le Cpk devrait-il être différent de 1,00 dans cet exemple de 1000 échantillons pour dire qu'il n'est pas statistiquement égal à 1,00 ? La figure 4 nous montre que le Cpk devrait être de 0,95 (ou 1,05) pour être statistiquement différent de 1,00.​

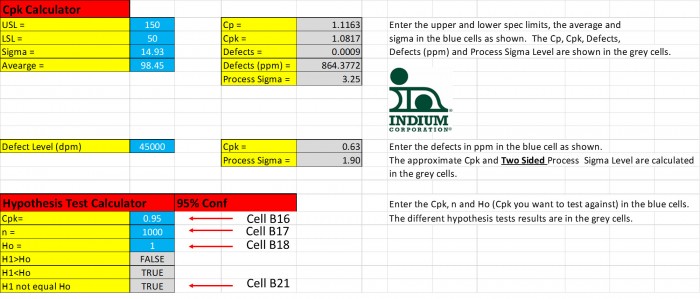
Figure 4. Si le Cpk n'est que de 0,95, ce Cpk est statistiquement différent d'un Cpk = 1,00.​

Cette feuille de calcul devrait être utile à ceux qui s'intéressent à la surveillance des Cpk relatifs à l'efficacité du transfert afin de réduire les défauts de soudure en fin de ligne. J'enverrai une copie de cette feuille de calcul aux lecteurs intéressés. Si vous souhaitez une copie, faites-en la demande en m'écrivant à rlasky@indium.com.

Merci,

Docteur Ron