Uso de las gráficas C para conjuntos de datos de diferentes tamaños

Amigos,

Las gráficas C son tablas de control utilizadas para rastrear los datos de atributos. Como un ejemplo, suponga que se encuentra rastreando defectos al final de un proceso de ensamble SMT. La gerencia ha indicado que desean conocer cuántos defectos existen por cada 10.000 ensamblajes. Así pues, por cada 10.000 ensamblajes fabricados, se rastrea la cantidad de defectos. Asumamos que, como ingeniero principal de proceso, ha estado recolectando estos datos de atributos por 6 meses. Para hacer el análisis simple, supongamos también que este es el número de ensamblajes que se fabrican cada día. En la figura 1 se muestran los datos de la gráfica C.  Casi con certeza la violación anotada a la Regla 1 de Shewhart se debe a la variación de causa común.

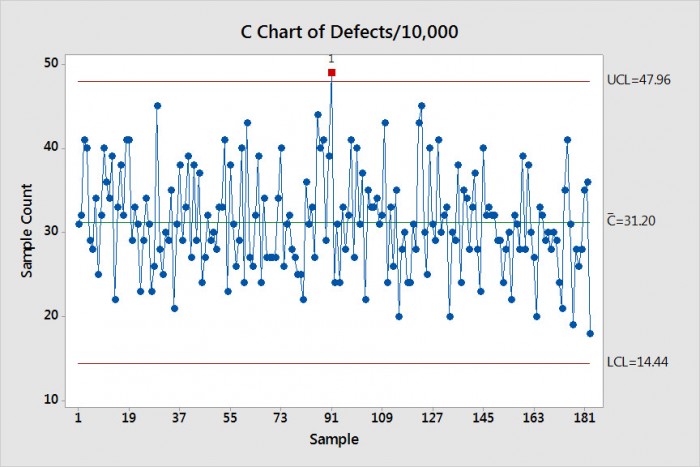
Figura 1. Datos de la Gráfica C para conjuntos de 10.000.​

Usted se dirige a unas vacaciones de dos semanas y algunos de sus colegas sobrecargados acuerdan supervisar la línea y recoger los datos de atributos. Lamentablemente, debido a su ausencia, hay algunos problemas de proceso en la línea de ensamble.  Como resultado, sólo 5.000 ensamblajes se producen cada día. La gerencia quiere comparar los nuevos datos con los antiguos, pero los tamaños de la muestra son diferentes. Es razonable simplemente multiplicar el número de defectos por 5.000 por la proporción de los tamaños de muestra, en este caso la relación es 2 (10.000/5.000).  Estos nuevos datos modificados se pueden agregar a los datos antiguos para trazar una gráfica C actualizada. En nuestro caso, los tres primeros días de datos de defectos fueron 31, 23 y 21 defectos por cada 5.000 ensamblajes. Multiplicados por 2, estos puntos de datos ahora se convierten en 62, 46 y 42. Realizar esta sencilla operación en los datos de dos semanas y sumarlos a los resultados de la gráfica C anterior resulta en la nueva gráfica C en la figura 2.

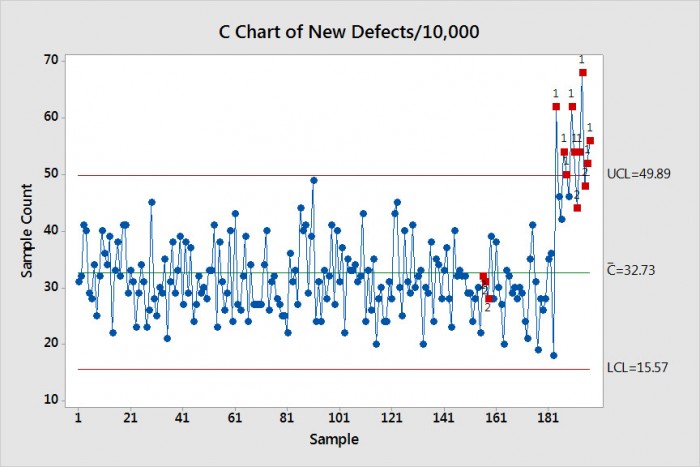
Figura 2. Mediante la multiplicación por 2 de cada uno de los números de fallos en el nuevo conjunto de datos, podemos agregar los nuevos datos a los datos antiguos y generar una nueva gráfica C. Tenga en cuenta que la tasa de defectos para los nuevos datos es mayor como lo atestiguan las muchas violaciones de la Regla 1 de Shewhart.

Tenga en cuenta que la tasa de defectos para los nuevos datos es mayor como lo atestiguan las muchas violaciones de la Regla 1 de Shewhart. Estos resultados apoyan firmemente el buen trabajo que debe realizar para apoyar el proceso de ensamblaje. No sólo la producción bajó 50%, sino que la tasa de defectos subió significativamente durante su ausencia.

He desarrollado una hoja de cálculo de Excel para realizar estas conversiones de datos. Si usted está interesado, envíeme un correo electrónico y le enviaré la hoja de cálculo.

Saludos,

Dr. Ron