“통계적인 중요성” 대 “실질적인 중요성”

여러분,

지난 가을의 선거를 따라가면서, 우리는 종종 특정 여론 조사가 통계적으로 중요하거나 그렇지 않다고 들었어요. 일례로서, 후보자 A는 1,000 명 중 51%에서 49% 득표로 후보자 B를 이끌었지만, 오차 범위 (MOE)가 3%를 약간 넘었기 때문에 결과는 통계적으로 중요하지 않았어요. 이와 같은 예는 사람들에게 당연히 통계적인 중요성의 의미를 주죠. 그렇지만, 매우 큰 표본 크기로서, 이 중요성은 오해의 소지가 있을 수 있어요. 제가 이전에 이 주제로 게시 글을 올렸지만, 특히 양적인 예에서, 반복적인 부분이 있어요.

이 사례로, SMT 업계의 일부 데이터를 살펴보기로 해요. 한 엔지니어가 전달 효율 (TE)에 대한 그들의 성능에 3가지 솔더 페이스트를 평가하기 원한다고 가정해 보죠. 목표 값은 100%에요. 페이스트 1은 98%의 TE, 페이스트 2는 97%의 TE를 가지며, 페이스트 3은 86%과 같은 TE가 나와요. 모든 페이스트들에서 데이터는 20%의 표준 편차를 가져요. 안타깝게도, 그녀의 회사는 아직 현대적인 SPI (솔더 페이스트 검사) 유형의 용량 측정 장비를 구매하지 않았고, 따라서 그녀는 모든 솔더 페이스트 증착 용량을 현미경으로 측정해야만 하죠. 따라서, 그녀는 단지 각 페이스트에 대해 20개 샘플만을 측정해요. 위의 데이터와 각 20개의 샘플로 그녀는 일부 통계 계산을 수행할 수 있고, 95%의 신뢰도로, 페이스트 1과 2 사이 TE에서 통계적으로 중요한 차이는 없지만, 두 페이스트 모두 페이스트 3보다 우수하게 나타나요.

그러나, 한 달 후 그녀의 회사는 SPI 도구를 구입합니다. 그것은 솔더 페이스트 증착물을 매우 빠르게 스캔하므로 그녀는 3가지 페이스트 각각에 대한 20,000개의 증착물을 스캔할 수 있어요. SPI가 정확하게 같은 결과를 생성한다는 것이 위안이 되요. 즉, 페이스트 1은 98 %의 TE를 가지며, 페이스트 2의 TE는 97 %이고, 페이스트 3은 86 %의 TE를 갖죠. 모든 페이스트들은 여전히 20%의 표준 편차를 나타내요.

따라서, 우리는 같은 결과를 갖은 것이 맞아요? 음, 아니에요. 물론 페이스트 1과 2는 여전히 페이스트 3보다 낫지만, 이 경우에서, 페이스트 1은 이제 통계적으로 페이스트 2보다 우수해요. 사실, 페이스트 2가 97.67%의 TE로 유입되었더라도, 페이스트 1은 95%의 신뢰도로 페이스트 2보다 통계적으로 우수하게 될 수 있어요.

이 변화의 원인이 무엇인가요? 그것은 샘플 크기와 관련이 있어요. 95% 평균 신뢰 구간 (CIM)은 부분적으로, 표준 편차를 샘플 크기의 제곱근으로 나눈 값으로 결정되었어요. 이 용어는 평균의 표준 오차 (SEM)라고 해요.

표본 크기가 올라갈 수록 SEM은 더 작아져요. 도표 1은 샘플 크기가 20일 때 페이스트 1과 2에 대한 평균의 샘플링 분포의 비교를 나타내고, 도표 2는 샘플 크기가 20,000일 때를 나타내요. 각 분포에 대한 평균의 신뢰 구간은 화살표가 있는 선으로 나타나 있어요. 도표 1에서, 20의 샘플 크기에 대한, 그 CIM은 크게 겹쳐지므로, 통계적인 차이가 없는 것을 제안하는 것을 주목하세요. 반면에, 도표 2에서, CIM은 폭넓게 분리되어 있고, 두 분포는 통계적으로 큰 차이가 있는 것을 나타내요.

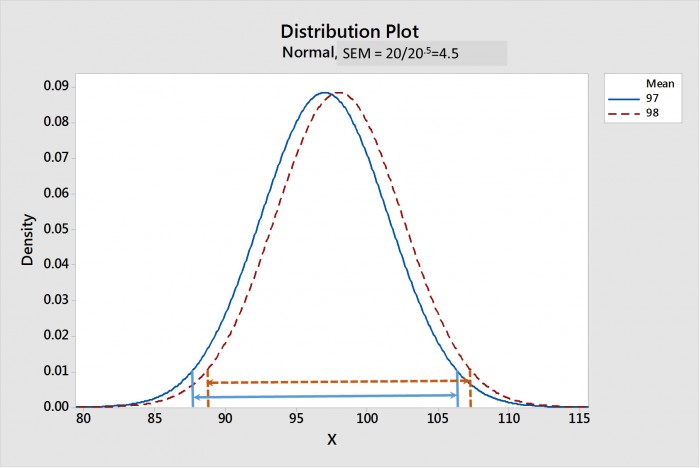
도표 1. 20의 샘플 크기로 페이스트 1과 2에 대한 평균의 샘플링 분포. 95% 평균의 신뢰 구간 (CIM)은 화살표 선으로 나타나 있어요. CIM이 겹쳐진 것은 통계적인 차이가 없음을 나타내는 것을 주목하세요.

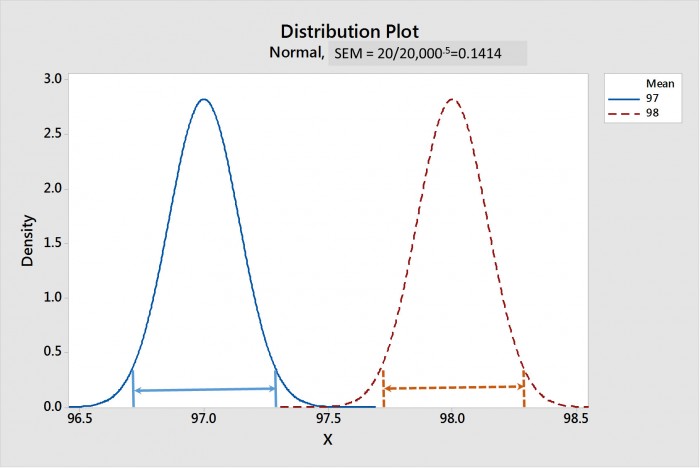
도표 2. 20,000의 샘플 크기로 페이스트 1과 2에 대한 평균의 샘플링 분포. 95% 평균의 신뢰 구간 (CIM)은 화살표 선으로 나타나 있어요. CIM이 겹쳐지지 않은 것은 통계적으로 큰 차이가 있는 것을 제안하는 것을 주목하세요.

이 상황은 어디에 우리를 남겨두나요?

분명히 20,000의 표본 크기가 98%의 평균 TE와 97.67% 중 하나 사이에 통계적으로 중요한 차이가 있다고 말할 수 있는 경우, 우리는 그 값을 질문해야 해요. 예를 들어, 경영진이 TE가 솔더 페이스트 구매에서 가장 중요한 매개변수라고 판단했다고 가정해 보죠. 또한 페이스트 1은 98% TE를 가지며 페이스트 2는 통계적으로 다른 97.67% TE를 가진다고 가정해 봅시다. 그렇지만, 페이스트 1은 일시 중지에 대한 응답이 매우 나빠요. 또한 다른 모든 성능 메트릭스는 동일하다고 가정해 보죠. 이 경우에서 저는 페이스트 1과 2의 TE가 “실제적인 중요성” 차이가 없다고 주장하고 싶고 동일하게 간주해야 해요. 페이스트 2의 성능을 일시 중지하는 우수한 응답을 추가하면 그것이 우승자가 됩니다.

“실제적인 중요성”은 어떻게 결정되나요? 사례에 따라 다르겠지만, 저는 2에서 5%에서 차이 범위는 실제적으로 중요하지 않다고 주장하고 싶어요. 대부분의 경우에서, 공학은 일부 실험으로 “실제적인 중요성”을 결정해야 해요. 그러나, SPI 장비와 같은 현대적인 도구로, 그것은 수 천 데이터 포인트를 측정할 수 있고, 저는 통계적이고 실제적인 차이 이분법이 점점 더 보편화되는 것을 이해할 필요가 있음을 볼 수 있어요.

제가 최근에 20,000 이상의 샘플 크기로 일부 TE 데이터를 분석한 직후 이 상황이 저에게 더욱 실제로 되었어요.

감사합니다,

론 박사