“Statistiquement significatif” vs “Pratiquement significatif”

Les amis,

Lors des élections à l'automne dernier, nous avons souvent entendu qu'un sondage particulier était ou n'était pas statistiquement significatif. À titre d'exemple, le candidat A mène devant le candidat B dans un sondage de 1000 personnes de 51 à 49 %, mais les résultats ne sont pas statistiquement significatifs étant donné que la marge d'erreur d'erreur est d'un peu plus de 3 %. Des exemples comme celui-ci donnent à juste titre à la significativité statistique le sens d'importance. Cependant, avec de très grandes tailles d'échantillons, cette signification peut induire en erreur . J'ai déjà écrit un article de blog sur ce sujet, mais il est bon de se répéter, en particulier avec un exemple quantitatif.

Pour cet exemple, regardons certaines données de l'industrie des CMS. Supposons qu'un ingénieur veuille évaluer les performances de 3 crèmes à souder au niveau de l'efficacité du transfert thermique (TE).La valeur cible est de 100 %. La crème 1 a une TE de 98 %, la crème 2 a un TE de 97 %, et la crème 3 a un TE égal à 86 %. Les données sur l'ensemble des crèmes ont un écart-type de 20 %. Malheureusement, la compagnie où elle travaille n'a pas encore acheté un SPI (dispositif d'inspection de crèmes à souder) servant à la mesure de volumes, elle doit donc mesurer tous les volumes de dépôts de crème de soudure à l'aide d'un microscope. Ainsi, elle ne mesure que vingt échantillons pour chaque crème. Avec les données ci-dessus et 20 échantillons de chaque crème, elle peut effectuer quelques calculs statistiques et montrer, avec une confiance de 95 %, qu'il n'y a pas de différence statistiquement significative de TE entre les crèmes 1 et 2, mais que les deux crèmes sont supérieures à la crème 3.

Cependant, un mois plus tard, son entreprise a acheté un outil SPI. Il peut analyser les dépôts de crème à souder si rapidement qu'elle traite 20 000 dépôts pour chacune des 3 crèmes. Le SPI donne exactement les mêmes résultats et c'est réconfortant, à savoir que la crème 1 a une TE de 98 %, la crème 2 a une TE de 97 %, et la crème 3 a une TE égale à 86 %. Toutes les crèmes montrent à nouveau un écart-type de 20 %.

Ainsi, nous obtenons les mêmes résultats, non ? Eh bien, non. Bien-sûr les crèmes 1 et 2 battent encore la crème 3 mais, dans ce cas, la crème 1 est maintenant statistiquement supérieure à la crème 2. En fait, même si la crème 2 obtenait une TE de 97,67 %, la crème 1 serait statistiquement supérieure à la crème 2 avec une confiance de 95 %.

Quelles sont les causes de ce nouveau résultat ? Il est lié à la taille de l'échantillon. L'intervalle de confiance de la moyenne (CIM) est déterminé, en partie, par l'écart type divisé par la racine carrée de la taille de l'échantillon. Ce terme est appelé l'erruer type de la moyenne (ETM).

À mesure que la taille de l'échantillon augmente, l'ETM diminue. La figure 1 montre une comparaison des distributions d'échantillonnage des moyennes pour les crèmes 1 et 2 avec une taille d'échantillon de 20 ; la figure 2 se rapporte à une taille d'échantillon de 20 000. Les intervalles de confiance de la moyenne pour chaque distribution sont indiqués par des lignes terminées par des flèches. Notez que, pour une taille d'échantillon de 20, dans la figure 1, les ICM se chevauchent grandement, ce qui suggère qu'il n'y a pas de différence statistique. Alors que, dans la figure 2, les ICM sont largement séparés, ce qui suggère que ces deux distributions sont très différentes statistiquement.​

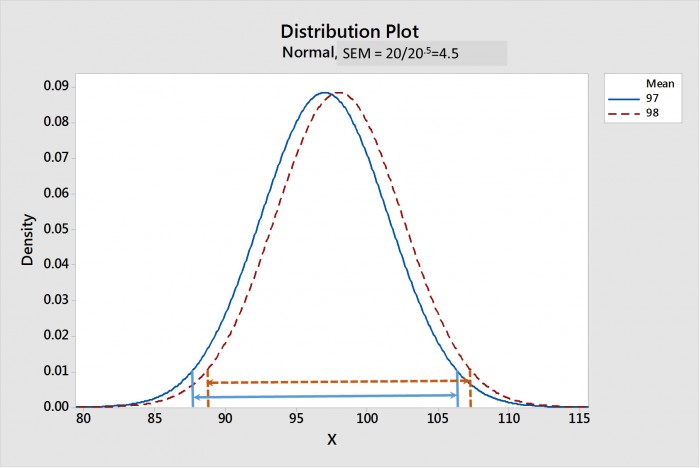
Figure 1. La distribution d'échantillonnage des moyennes pour les crèmes 1 et 2 avec une taille d'échantillon de 20. Les intervalles de confiance de 95 % des moyennes (ICM) sont représentés par les lignes terminées par des flèches. Notez que les ICM se chevauchent, ce qui ne suggère aucune différence statistique.​

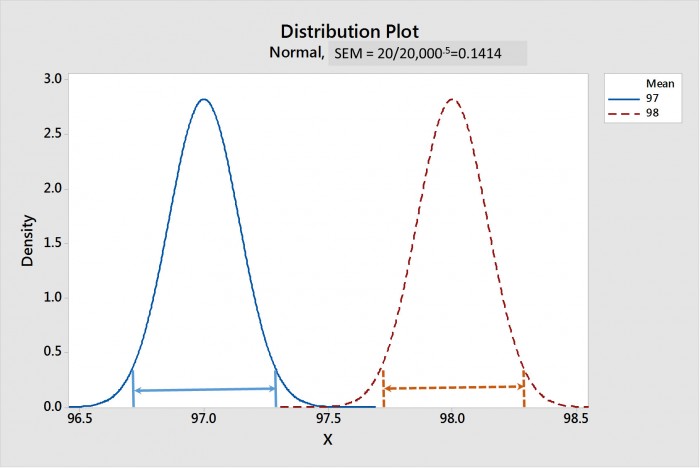
Figure 2. La distribution d'échantillonnage des moyennes pour les crèmes 1 et 2 avec une taille d'échantillon de 20 000. Les intervalles de confiance de 95 % des moyennes (ICM) sont représentés par les lignes terminées par des flèches. Notez que les CIM ne se chevauchent pas, ce qui suggère une forte différence statistique​

Où cette situation nous mène-t-elle ?

De toute évidence, si une taille d'échantillon de 20 000 nous permet de dire qu'il existe une différence statistiquement significative entre une TE moyenne de 98 % et une TE de 97,67 %, nous devons remettre en question sa valeur. À titre d'exemple, supposons que la direction a décidé que la TE représente le paramètre le plus important lors de l'achat d'une crème à souder. Supposons de plus que la crème 1 ait une TE de 98 % et que la crème 2 ait une TE statistiquement différente de 97,67 %. Cependant, la crème 1 a une réponse très médiocre à la pause. Supposons aussi que toutes les autres mesures de performance sont les mêmes. Dans ce cas, je dirais que les TE des crèmes 1 et 2 ne sont pas "pratiquement et significativement" différentes et devraient être considérées comme étant identiques. Si de plus on ajoute la réponse supérieure en matière de performance de pause de la crème 2, elle devrait sortir gagnante.

Comment la "signification pratique" est-elle déterminée ? Cela varie d'un cas à l'autre, mais je dirais qu'une différence de TE de l'ordre de 2 à 5 % n'est pas pratiquement significative. Dans la plupart des cas, l'ingénierie devrait déterminer la "signification pratique" à l'appui de certaines expériences. Cependant, avec des outils modernes comme les dispositifs SPI, qui peuvent mesurer des milliers de données mesurées, je vois la nécessité de mieux comprendre la dichotomie entre les différences statistiques et pratiques, laquelle devient de plus en plus courante.

Cette situation m'est apparue comme étant plus réelle depuis que j'ai récemment analysé certaines données de TE avec des échantillons de plus de 20 000 pièces.

Merci,

Docteur Ron