„Statistisch signifikant“ vs. „in der Praxis signifikant“

Leute,

bei den Wahlen im letzten Jahr wurde oft gesagt, eine bestimmte Umfrage sei statistisch signifikant bzw. nicht signifikant gewesen. Beispielsweise führte Kandidat A bei einer Befragung von 1.000 Personen 51 zu 49 % gegenüber Kandidat B, das Ergebnis war statistisch jedoch nicht signifikant, da die Fehlermarge (MOE) etwas über 3 % lag. Beispiele wie dieses verleihen der statistischen Signifikanz zu Recht eine gewisse Bedeutung. Bei sehr großen Stichprobengrößen kann diese Signifikanz jedoch irreführend sein. Ich habe zu diesem Thema bereits in Blog-Beiträgen berichtet. Es ist jedoch sinnvoll, erneut auf dieses Thema einzugehen, insbesondere mit einem quantitativen Beispiel.

Lassen Sie uns dazu einige Daten aus der SMT-Branche betrachten. Nehmen wir an, eine Ingenieurin möchte die Leistung von 3 Lotpasten hinsichtlich der Übertragungseffizienz (TE) bewerten. Der Sollwert ist 100 %. Die Lotpaste 1 besitzt eine TE von 98 %, die Lotpaste 2 von 97 % und die Lotpaste 3 erreicht eine TE von 86 %. Die Daten aller Lotpasten besitzen eine Standardabweichung von 20 %. Leider hat ihr Unternehmen noch kein modernes Volumenmessgerät von der Art eines Lotpasteninspektionsgeräts (SPI) angeschafft, sodass sie den Umfang aller Lotpastendepots mit einem Mikroskop messen muss. Daher misst sie nur 20 Proben jeder Lotpaste. Mit den oben angegebenen Daten und jeweils 20 Proben kann sie einige statistische Berechnungen durchführen und mit einer Konfidenz von 95 % nachweisen, dass zwischen der Lotpaste 1 und 2 kein statistisch signifikanter Unterschied bezüglich der TE besteht, dass beide Lotpasten jedoch gegenüber der Lotpaste 3 überlegen sind.

Einen Monat später kauft ihr Unternehmen endlich das SPI-Gerät. Es kann Lotpastendepots so schnell scannen, dass sie jeweils 20.000 Depots der 3 Pasten misst. Es ist beruhigend, dass das SPI-Gerät dieselben Ergebnisse produziert, d. h. die Lotpaste 1 besitzt eine TE von 98 %, die Lotpaste 2 von 97 % und die TE der Lotpaste 3 entspricht 86 %. Alle Lotpasten weisen weiterhin eine Standardabweichung von 20 % auf.

Wir erhalten somit dasselbe Resultat, oder? Nun ja, nicht unbedingt. Natürlich schlagen die Lotpasten 1 und 2 weiterhin die Lotpaste 3. Die Lotpaste 1 ist in diesem Fall jedoch der Lotpaste 2 statistisch überlegen. Selbst wenn die Lotpaste 2 eine TE von 97,67 % erreichen würde, wäre die Lotpaste 1 ihr mit einer Konfidenz von 95 % statistisch weiterhin überlegen.

Was ist die Ursache dieses Unterschieds? Er hat mit der Stichprobengröße zu tun. Das Konfidenzintervall des Mittelwerts (CIM) von 95 % wird teilweise von der Standardabweichung dividiert durch die Quadratwurzel der Stichprobengröße bestimmt. Dieser Begriff wird Standardfehler des Mittelwerts (SEM) genannt.

Bei Zunahme der Stichprobengröße wird der SEM kleiner. Abbildung 1 zeigt einen Vergleich der Stichprobenverteilung des Mittelwerts der Lotpasten 1 und 2 bei einer Stichprobengröße von 20; die Abbildung 2 zeigt denselben Vergleich bei einer Stichprobengröße von 20.000. Die Konfidenzintervalle des Mittelwerts jeder Verteilung werden durch Linien mit Pfeilen darstellt. Beachten Sie, dass bei der Stichprobengröße 20 die CIMs auf der Abbildung 1 größtenteils überlappen, was vermuten lässt, dass kein statistischer Unterschied vorliegt. Auf der Abbildung 2 sind die CIMs dagegen weit voneinander entfernt und deuten darauf hin, dass diese beiden Verteilungen statistisch stark unterschiedlich sind.

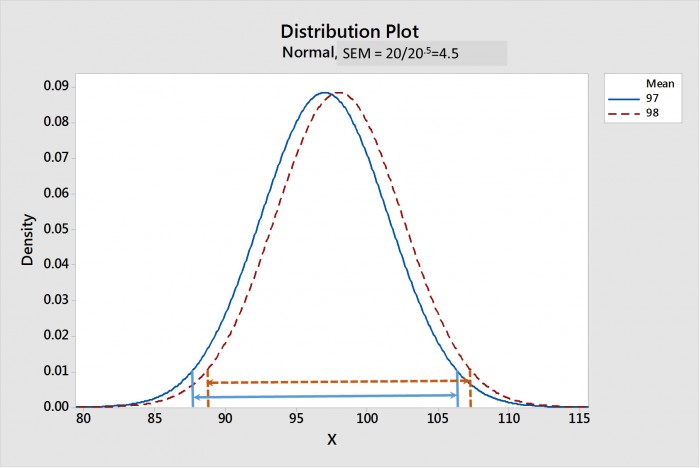
Abbildung 1. Die Stichprobenverteilung des Mittelwerts der Lotpasten 1 und 2 bei einer Stichprobengröße von 20. Die 95%igen Konfidenzintervalle des Mittelwerts (CIMs) jeder Verteilung werden durch Linien mit Pfeilen darstellt. Beachten Sie, dass die CIMs überlappen, was vermuten lässt, dass kein statistischer Unterschied vorliegt.

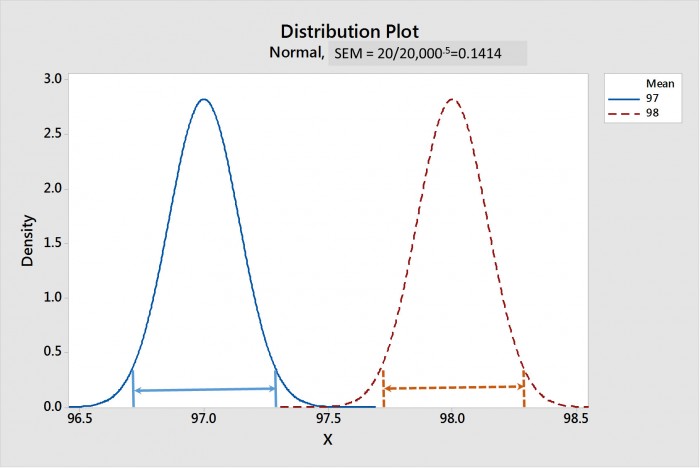
Abbildung 2. Die Stichprobenverteilung des Mittelwerts der Lotpasten 1 und 2 bei einer Stichprobengröße von 20.000. Die 95%igen Konfidenzintervalle des Mittelwerts (CIMs) jeder Verteilung werden durch Linien mit Pfeilen darstellt. Beachten Sie, dass die CIMs jetzt überlappen und auf einen starken statistischen Unterschied hindeuten.

Was bedeutet dies alles nun?

Wenn eine Stichprobengröße von 20.000 uns zu der Aussage berechtigt, dass ein statistisch signifikanter Unterschied zwischen einer durchschnittlichen TE von 98 % und einer von 97,67 % besteht, sollten wir den Wert dieser Aussage sicherlich infrage stellen. Nehmen wir beispielsweise an, die Geschäftsführung hat die TE als den wichtigsten Parameter beim Einkauf einer Lotpaste festgelegt. Nehmen wir weiterhin an, die Lotpaste 1 besitzt eine TE von 98 % und die Lotpaste 2 die statistisch unterschiedliche TE von 97,67 %. Die Lotpaste 1 weist jedoch eine sehr schlechte Reaktion bei Stillstandszeiten zwischen zwei Drucken auf. Nehmen wir außerdem an, alle anderen Leistungskennzahlen sind gleich. In diesem Fall würde ich argumentieren, dass die TEs der Lotpasten 1 und 2 nicht „in der Praxis signifikant“ sind und daher gleich bewertet werden sollten. Unter Berücksichtigung der überlegenen Reaktion bei Stillstandszeiten wäre die Lotpaste 2 somit der Sieger.

Wie wird „in der Praxis signifikant“ bestimmt? Das variiert von Fall zu Fall. Ich würde jedoch sagen, dass eine TE-Differenz im Bereich von 2 bis 5 % in der Praxis nicht signifikant ist. In den meisten Fällen sollte die technische Abteilung die „Signifikanz in der Praxis“ anhand von Versuchen bestimmen. Angesichts der modernen Werkzeuge wie SPI-Geräte, die Tausende von Datenpunkten messen können, verstehe ich jedoch, dass das Bedürfnis, die Gegensätzlichkeit zwischen der statistischen und praktischen Differenz zu verstehen, immer wichtiger wird.

Diese Situation wurde mir bewusst, da ich kürzlich einige TE-Daten mit Stichprobengrößen über 20.000 analysieren musste.

Danke,

Dr. Ron