“Estadísticamente significativo” contra “Prácticamente significativo”

Amigos,

Durante el seguimiento de las elecciones el otoño pasado, con frecuencia escuchamos que alguna votación era o no era estadísticamente significativa. Por ejemplo, el candidato A adelantaba al candidato B en una votación de 1000 personas en 51 a 49%, pero los resultados no eran estadísticamente significativos debido a que el margen de error (MOE) era menor que el 3%. Ejemplos como éste ameritan que se le otorgue un sentido de importancia a la significatividad estadística. Sin embargo, con tamaños de muestra muy grandes, tal significatividad puede ser engañosa. He escrito sobre este tema antes, pero vale la pena repetirlo, especialmente con un ejemplo cuantitativo.

Para este ejemplo, veamos algunos datos de la industria SMT. Supongamos que una ingeniera quiere evaluar el rendimiento de eficiencia de transferencia (TE) de 3 pastas de soldadura. El valor objetivo es 100%. La pasta 1 tiene una TE del 98%, la TE de la pasta 2 es del 97% y la pasta 3 viene con una TE igual al 86%. Los datos de todas las pastas tienen una desviación estándar del 20%. Por desgracia, su empresa todavía tiene que comprar un tipo de dispositivo moderno de medición de volumen SPI (inspección de pasta de soldadura), por lo que tiene que medir todos los volúmenes de depósito de pasta de soldadura con un microscopio. Así pues, ella solo mide veinte muestras de cada pasta. Con los datos anteriores y 20 muestras de cada pasta, ella puede realizar algunos cálculos estadísticos y mostrar, con una confianza del 95%, que no hay diferencia estadísticamente significativa en TE entre las pastas 1 y 2, pero que ambas pastas son superiores a la pasta 3.

Sin embargo, un mes después su empresa compró una herramienta SPI. Dicha herramienta puede escanear depósitos de pasta tan rápidamente que ella escaneó 20.000 depósitos para cada una de las 3 pastas. Es reconfortante saber que la SPI produce exactamente los mismos resultados, es decir, la pasta 1 tiene una TE del 98%, la TE de la pasta 2 es del 97% y la pasta 3 tiene una TE igual al 86%. Aun así, todas las pastas todavía muestran una desviación estándar del 20%.

Entonces, tenemos los mismos resultados, ¿cierto? Bueno, no. Por supuesto que las pastas 1 y 2 aun vencen a la pasta 3, pero, en este caso, la pasta 1 ahora es estadísticamente superior a la pasta 2. De hecho, incluso si la pasta 2 tuviese una TE del 97,67%, la pasta 1 sería estadísticamente superior a la pasta 2 con una confianza del 95%.

¿Cuál es la causa de este cambio? Se relaciona con el tamaño de la muestra. El intervalo de confianza del 95% de la media (CIM) se determina, en parte, al dividir la desviación estándar por la raíz cuadrada del tamaño de la muestra. A este término se le conoce como el error estándar de la media (SEM).

A medida que aumenta el tamaño de la muestra, el SEM disminuye. La Figura 1 muestra una comparación de las distribuciones de muestra de las medias para las pastas 1 y 2 cuando el tamaño de la muestra es 20; la figura 2 muestra lo mismo cuando el tamaño de la muestra es 20.000. Los intervalos de confianza de la media para cada distribución se muestran mediante líneas con puntas de flecha. Tenga en cuenta que, para un tamaño de muestra de 20, en la Figura 1, los CIM se superponen fuertemente, lo que sugiere que no hay diferencia estadística. Mientras que, en la Figura 2, los CIM están ampliamente separados, lo que sugiere que estas dos distribuciones son fuertemente diferentes en términos estadísticos.

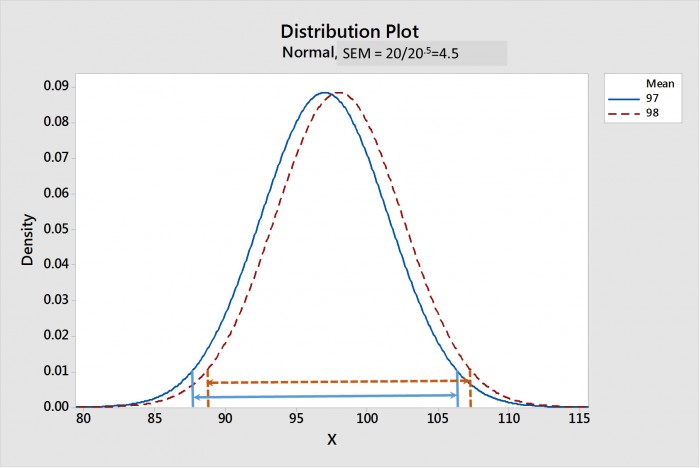
Figura 1. Distribución de muestreo de las medias para las pastas 1 y 2 con un tamaño de muestra de 20. Los intervalos de confianza del 95% de las medias (CIM) se muestran mediante líneas con flechas. Tenga en cuenta que los CIM se superponen, lo que sugiere que no hay diferencia estadística.

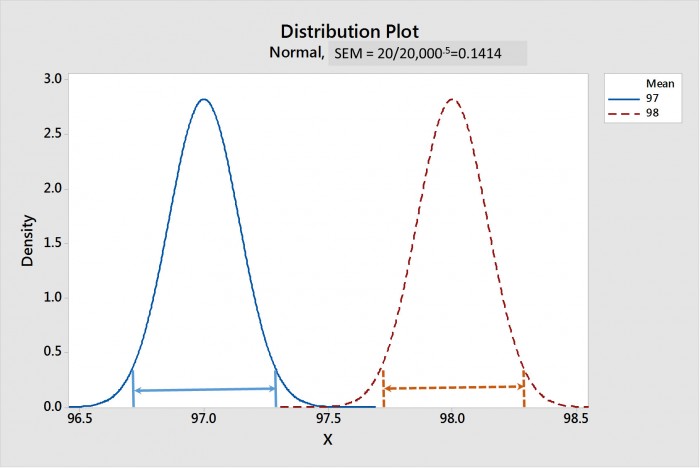
Figura 2. Distribución de muestreo de las medias para las pastas 1 y 2 con un tamaño de muestra de 20.000. Los intervalos de confianza del 95% de las medias (CIM) se muestran mediante líneas con flechas. Tenga en cuenta que los CIM no se superponen, lo que sugiere una fuerte diferencia estadística.

¿En qué punto nos deja esta situación?

Es evidente que si un tamaño de muestra de 20.000 nos permite decir que hay una diferencia estadísticamente significativa entre un TE promedio de 98% y uno de 97,67% entonces tenemos que cuestionar su valor. Por ejemplo, supongamos que la gerencia ha determinado que TE es el parámetro más crítico en la compra de una pasta de soldadura. Supongamos también que la pasta 1 tiene un TE del 98% y que la pasta 2 tiene un TE del 97,67% estadísticamente diferente. Sin embargo, la pasta 1 tiene una respuesta muy pobre a la pausa. Supongamos asimismo que todas las demás métricas de rendimiento son las mismas. En este caso, yo diría que los TE de las pastas 1 y 2 no son "en la práctica significativamente" diferentes y se deben considerar como iguales. Añadir la respuesta superior a rendimiento en pausa de la pasta 2 debe hacer que dicha pasta sea la ganadora.

¿Cómo se determina la “significatividad práctica”? Variará de un caso a otro, pero yo diría que, con TE, una diferencia en el rango de 2 a 5% no es prácticamente significativa. En la mayoría de los casos, la ingeniería debe determinar la "significatividad práctica" mediante algunos experimentos. Sin embargo, con herramientas modernas como los dispositivos SPI, que pueden medir miles de puntos de datos, puedo ver la necesidad de entender la dicotomía entre la diferencia estadística y la práctica que es cada vez más común.

Esta situación se hizo más real para mí, puesto que acabo de analizar algunos datos de TE con tamaños de muestra de más de 20.000.

Saludos,

Dr. Ron